persamaan kuadrat dan fungsi kuadrat adalah salah dua materi yang diajarkan pada mata pelajaran Matematika. Biasanya, Sedulur akan menjumpai materi ini ketika duduk di bangku kelas 9 SMP dan dilanjutkan di SMA.
Secara umum, materi ini membahas tentang persamaan suku banyak dengan pangkat tertingginya adalah dua. Ingin mengetahui lebih lanjut soal persamaan kuadrat? Simak penjelasan selengkapnya berikut ini.
BACA JUGA: 20 Manfaat Buah Naga yang Baik untuk Kesehatan Tubuh
1. Pengertian

Sebelum membahas lebih rinci, Sedulur perlu untuk memahami terlebih dahulu mengenai pengertiannya. Dirangkum dari berbagai sumber, persamaan kuadrat adalah persamaan suku banyak atau biasa disebut polinominal yang variabelnya memiliki pangkat tertinggi sama dengan dua (2). Contohnya adalah sebagai berikut:
2x² + 3x + 4
Dapat dilihat bahwa pada persamaan di atas terdapat variabel yang memilik pangkat dua. Sehingga bisa dinyatakan persamaan kuadrat berbeda dengan persamaan linier yang pangkat tertingginya adalah satu (1).
BACA JUGA: 10 Rekomendasi Bak Mandi Minimalis Terbaik dan Kekinian
2. Bentuk umum

Untuk mengetahui bentuk umum persamaan kuadrat, kita bisa menguraikan contoh pada poin sebelumnya, yaitu:
2x² + 3x + 4 = 0
Keterangan:
Angka 2 (dua) di depan x² dan angka 3 (tiga) di depan x adalah koefisien
x adalah variabel
Seperti yang dijelaskan sebelumnya, variabel pada persamaan kuadrat memiliki pangkat tertinggi sama dengan dua. Diketahui pada contoh di atas variabelnya terdiri atas x berpangkat satu dan x berpangkat dua. Sementara, angka 4 adalah konstanta.
Dalam bentuk umum persamaan kuadrat, koefisian dilambangkan dengan a dan b. Sedangkan konstanta dilambangkan dengan c. Sehingga bentuk umum persamaan kuadrat bisa dituliskan sebagai ax² + bx + c = 0
Keterangan:
- a, b = koefisien (a tidak sama dengan 0)
- x = variabel
- c = konstanta
BACA JUGA: Mengenal Quotex Aplikasi Trading Ilegal, Biar Kita Tidak Tertipu
3. Jenis

Setelah mengetahui definisi dan bentuk umumnya, Sedulur juga perlu memahami jenisnya. Secara umum, persamaan kuadrat dibagi menjadi empat jenis yakni sebagai berikut.
1. Persamaan kuadrat biasa adalah yang nilai koefisien a adalah 1. Contohnya sebagai berikut: x² + 3x + 4 = 0
2. Persamaan kuadrat murni ditandai dengan nilai b yang sama dengan 0. Berikut contohnya: x² + 4 = 0
3. Persamaan kuadrat tak lengkap. Apabila murni nilai b adalah 0, maka pada persamaan kuadrat tak lengkap nilai c yang sama dengan 0. Lihat contoh berikut: x² + 3x = 0
4. Persamaan kuadrat rasional adalah yang nilai koefisien (a dan b) dan konstantanya (c) berupa bilangan rasional. Misalnya 2x² + 3x + 4 = 0
BACA JUGA: Memahami Arti Passion Beserta Cara Menemukannya
4. Faktorisasi
Persamaan kuadrat faktorisasi atau pemfaktoran adalah cara yang digunakan untuk menemukan akar kuadrat. Caranya adalah dengan mengubah penjumlahan suku-suku aljabar menjadi bentuk perkalian. Contoh:
ax² + bx + c = 0 diubah menjadi (x + p)(x + q)
Perlu diperhatikan, cara ini dapat digunakan dengan syarat:
b = hasil penjumlahan antara p dan q
c = hasil perkalian antara p dan q
Contoh soal: x² + 5x + 6 = 0
Bentuk faktorisasinya adalah (x + 3)(x + 2)
Sehingga, akarnya adalah x = -3 dan x = -2
BACA JUGA: Anak Sulung: Pengertian, Sifat, Fakta & Karakteristiknya
5. Persamaan kuadrat sempurna
Persamaan ini tak selalu bisa diselesaikan dengan cara pemfaktoran. Tapi Sedulur tak perlu khawatir karena terdapat cara lain yang bisa digunakan yaitu dengan melengkapi kuadrat sempurna. Rumusnya adalah sebagai berikut.
ax² + bx + c = 0 menjadi (x + p)² = q atau x + q = ±√q
Contoh soal:
x² + 8x + 6 = 0
x² + 8x = -6
Kemudian, tambahkan satu angka di ruas kiri dan kanan agar menjadi kuadrat sempurna. Angka yang ditambahkan diambil dari separuh angka koefisian dari x yang dikuadratkan sehingga persamaannya menjadi:
x² + 8x + 4² = -6 + 4²
x² + 8x + 16 = -6 + 16
x² + 8x + 16 = 10
(x + 4)(x + 4)² = 10
x + 4 = ±√10
x = ±√10 – 4
Maka, x adalah √10 – 4 atau -√10 – 4
BACA JUGA: Arti Anak Bungsu Beserta Fakta yang Perlu Diketahui Orang Tua
6. Rumus ABC persamaan kuadrat
Penyelesaian persamaan kuadrat juga bisa dilakukan dengan menggunakan rumus ABC. Cara ini memanfaatkan nilai dari a, b, dan c dari suatu persamaan. Berikut adalah hal-hal yang perlu diperhatikan untuk menyelesaikan persamaan dengan rumus ABC.
- Persamaan harus dinyatakan dalam bentuk ax² + bx + c = 0
- Tentukan nilai a, b, dan c
- Rumus:
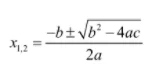
BACA JUGA: Internet adalah: Pengertian, Sejarah, Perkembangan & Manfaat
7. Jenis akar persamaan kuadrat

Berdasarkan nilai diskriminan (D), akar persamaan kuadrat dapat dibagi menjadi tiga jenis, sebagai berikut.
1. Akar real adalah yang memiliki nilai D lebih besar dari 0 atau D > 0.
2. Akar kembar atau juga disebut sebagai akar real sama adalah yang memiliki nilai D sama dengan 0 atau D = 0.
3. Akar imajiner. Kebalikan dari akar real, akar imajiner atau akar tidak real adalah yang bentuknya berupa angka imajiner. Sehingga nilai D lebih kecil dari 0 atau D < 0.
BACA JUGA: Tes MBTI: Pengertian, Penerapan & Macam Tipe Kepribadiannya
8. Diskriminan persamaan kuadrat
Diskriminan adalah suatu nilai yang menjadi penentu sifat-sifat akar dari suatu persamaan ini. Jenis ini ditentukan dengan cara mencari nilai diskriminan.
Rumus diskriminan ABC di mana D = b² – 4a
BACA JUGA: Negara Agraris: Pengertian, Keuntungan dan Potensinya
9. Persamaan kuadrat baru

Ini adalah suatu persamaan yang dibentuk berdasarkan akar dan berkaitan dengan akar persamaan lama. Untuk menyusunnya, Sedulur dapat menggunakan rumus jumlah dan hasil kali akar persamaan. Akarnya mempunyai hubungan yang beraturan dengan x1 dan x2 yang merupakan akar persamaan ax² + bx + c = 0.
BACA JUGA: 22 Inspirasi Taman Minimalis untuk Percantik Halaman Hunian
10. Penerapan persamaan kuadrat dalam kehidupan

Setelah memahami materi ini, Sedulur mungkin ingin tahu bagaimana penerapan teori tersebut dalam kehidupan sehari-hari. Berikut ini sudah dirangkum informasi selengkapnya.
1. Bidang olahraga misalnya pada cabang olahraga panahan, basket, dan sepak bola. Hal ini terjadi ketika seorang pemain melepaskan tendangan atau tembakan yang mana lintasannya membentuk sebuah garis melengkung. Gerakan yang dihasilkan ini disebut parabola yang meruapakan salah satu bentuk grafik persamaan ini.
2. Pelangi merupakan fenomena alam yang banyak dikagumi keindahannya. Sebab pelangi memiliki warna-warna yang cantik. Ternyata, pelangi bisa menjadi contoh penerapan persamaan ini karena membentuk sebuah kurva layaknya tendangan seorang pemain sepak bola.
Demikian tadi pembahasan seputar materi persamaan kuadrat. Semoga informasi ini dapat bermanfaat untuk Sedulur, ya!



