Sudut istimewa adalah salah satu istilah yang tentunya Sedulur sering dengar dalam dunia keilmuan matematika. Istilah tersebut sering muncul pada salah satu cabang matematika, trigonometri.
Kira-kira apa ya, yang dimaksud dengan sudut istimewa 53, 37, dan jenis-jenis lainnya? Simak pembahasan singkatnya berikut ini!
BACA JUGA: Penemu Matematika Beserta Biografi Singkatnya
Pengertian trigonometri sudut istimewa

Seperti yang telah diungkapkan sebelumnya, sudut istimewa merupakan salah satu istilah yang kerap kali muncul dalam bidang keilmuan matematika, terutama pada cabang trigonometri.
Trigonometri sendiri merupakan cabang dari matematika yang berfokus mempelajari hubungan antara panjang sisi dan sudut segitiga. Trigonometri pertama kali ditemukan pada 140 SM oleh Hipparchus. Ia juga dikenal sebagai “Bapak Trigonometri” dengan membuat tabel trigonometri untuk pertama kalinya.
Dalam trigonometri, nilai pasti dari sudut tertentu tidak bisa langsung ditemukan hanya dengan melihat rasio panjang sisinya. Namun, terdapat sejumlah sudut yang dapat ditemukan langsung dengan menggunakan perhitungan rasio. Sudut-sudut tersebut kemudian disebut dengan sudut istimewa.
Terdapat lima sudut tersebut dalam trigonometri, yaitu 0°, 30°, 45°, 60°, 90°. Hubungan trigonometri dari kelima sudut tadi dapat dilihat dalam tabel sudut istimewa di atas.
BACA JUGA: Persamaan Kuadrat dalam Matematika Beserta Contoh Soalnya
Trigonometri sudut istimewa 0°
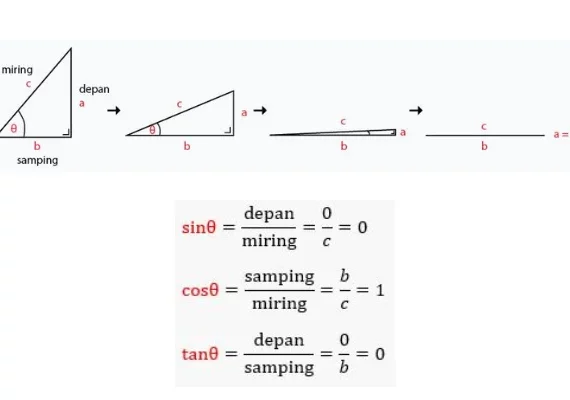
Sudut istimewa 0-360 yang pertama adalah 0°. Dalam sudut 0°, trigonometri membuat salah satu sudut dari θ menjadi 0° pada segitiga siku-sikunya. Alhasil, dengan sudut 0°, segitiga akan menjadi satu garis yang lurus. Panjang sisi samping b sama dengan sisi miring c. Panjang sisi depan a menjadi 0. Perhatikan gambar di atas.
Trigonometri sudut istimewa 30°
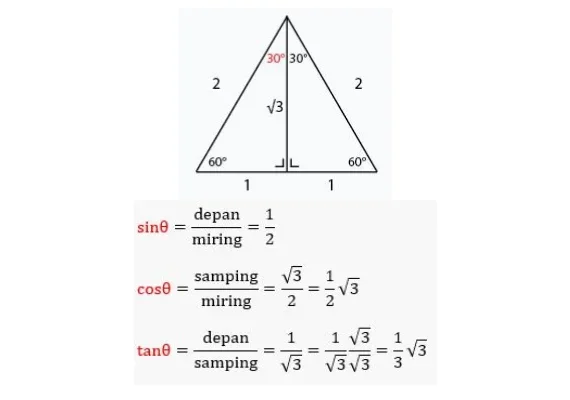
Dalam sudut 30°, trigonometri membuat salah satu sudut dari θ menjadi 30° pada segitiga siku-siku yang berasal dari segitiga sama sisi. Pemilihan panjang sisi miring dari segitiga sama sisi diambil dengan cara sesederhana mungkin, dengan nilai 2.
Angka 2 dipilih agar pada saat segitiga sama sisi dibagi menjadi dua untuk membentuk segitiga siku-siku, panjang salah satu sisinya akan menjadi 1. Jadi, pada salah satu sudut yang bernilai 30°, panjang sisi sampingnya akan bernilai √3 dalam teorema Phytagoras. Perhatikan gambar di atas.
BACA JUGA: Rumus Keliling Segitiga Beserta Pembahasan & Contoh Soalnya
Trigonometri sudut istimewa 45°
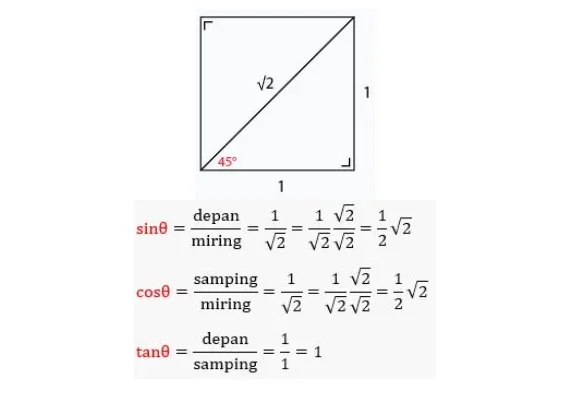
Dalam sudut 45°, trigonometri membuat salah satu sudut dari θ menjadi 45° pada segitiga siku-siku yang berasal dari persegi. Pemilihan panjang sisi dari segitiga sama sisi diambil dengan cara sesederhana mungkin, dengan nilai 1. Dengan mengacu pada sudut 45° tadi, panjang sisi miringnya akan bernilai √2 dalam teorema Phytagoras. Perhatikan gambar di atas.
Trigonometri sudut istimewa 60°
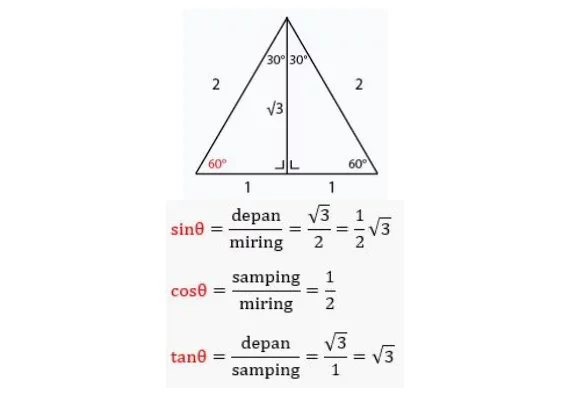
Dalam sudut 60°, trigonometri membuat salah satu sudut dari θ menjadi 60° pada segitiga siku-siku yang berasal dari segitiga sama sisi. Pemilihan panjang sisi miring dari segitiga sama sisi diambil dengan cara sesederhana mungkin, dengan nilai 2.
Angka 2 dipilih agar pada saat segitiga sama sisi dibagi menjadi dua untuk membentuk segitiga siku-siku, panjang sisi sampingnya akan menjadi 1. Dengan mengacu pada sudut 60° tadi, panjang sisi depannya akan bernilai √3 dalam teorema Phytagoras. Perhatikan gambar di atas.
BACA JUGA: Rumus Volume Limas Segi Empat Beserta Contoh Soalnya
Trigonometri sudut istimewa 90°
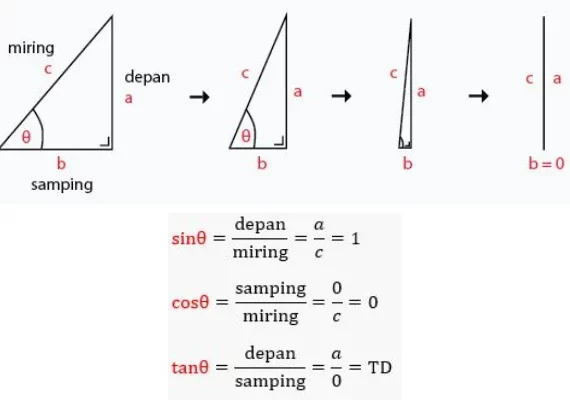
Dalam sudut 90°, trigonometri membuat salah satu sudut dari θ menjadi 900° pada segitiga siku-sikunya. Alhasil, dengan sudut 90°, segitiga akan menjadi satu garis yang lurus. Panjang sisi miring c sama dengan sisi depan a. Panjang sisi samping b menjadi 0. Perhatikan gambar di atas.
Contoh soal
Di bawah ini merupakan satu contoh soal sufut istimewa 27 dari diskusi yang telah dibahas di atas.
- sin 60° . cos 30° + cos 60° . sin 30° = …
(a) 1
(b) ½
(c) ½ √2
(d) ½
(e) 0
Jawaban:
sin 60° . cos 30° + cos 60° . sin 30°
= ½ √3 . ½ √3 + ½ . ½
= ¾ + ¼
= 1 atau (a)
Itu dia pembahasan mengenai sudut 0°, 30°, 45°, 60°, 90° trigonometri dengan tabel dan contoh soalnya. Seperti yang telah disebutkan sebelumnya, nilai pasti dari sudut tertentu dalam trigonometri tidak dapat langsung ditemukan hanya dengan melihat rasio panjang sisinya. Tetapi, sudut 0°, 30°, 45°, 60°, 90° dapat ditemukan langsung dengan menggunakan perhitungan rasio.
Pada kesempatan berikutnya, materi sudut istimewa kuadran 2 dan sudut-sudut lainnya. Semoga artikel ini dapat menambah pengetahuan Sedulur dalam trigonometri, ya!
Mau belanja bulanan nggak pakai ribet? Aplikasi Super solusinya! Mulai dari sembako hingga kebutuhan rumah tangga tersedia lengkap. Selain harganya murah, Sedulur juga bisa merasakan kemudahan belanja lewat handphone. Nggak perlu keluar rumah, belanjaan pun langsung diantar.
Bagi Sedulur yang punya toko kelontong atau warung, bisa juga lho belanja grosir atau kulakan lewat Aplikasi Super. Harga dijamin lebih murah dan bikin untung makin melimpah.



