Balok adalah salah satu bentuk bangun ruang. Bentuk bangun ruang ini banyak ditemukan dalam barang-barang di sekitar. Contoh saja kotak kardus, batu bata, hingga almari. Masalah bangun ruang ini sendiri dipelajari dalam matematika khususnya bidang geometri. Sehingga bisa disimpulkan pengetahuan mengenai balok termasuk ciri-ciri dan rumusnya penting untuk dipahami.
Ingin tahu lebih jauh tentang bangun ruang satu ini? Berikut telah dirangkum informasi lengkapnya untuk Sedulur. Simak sampai habis, ya!
BACA JUGA: Penemu Matematika Beserta Biografi Singkatnya
Definisi balok
Sebelum mempelajari tentang ciri-ciri hingga contohnya, tidak ada salahnya bagi Sedulur untuk memahami terlebih dahulu mengenai pengertiannya.
Dirangkum dari berbagai sumber, balok merupakan salah satu bentuk bangun ruang atau bangun tiga dimensi. Balok juga dikenal sebagai prisma segi empat. Bangun ruang ini dibentuk oleh enam persegi panjang. Setiap persegi panjang yang saling berhadapan memiliki ukuran yang sama. Sehingga bisa dikatakan terdapat tiga pasang persegi panjang yang membentuk bangun ruang balok.
Ciri-ciri
Setelah mengetahui definisi balok, mari kita cari tahu tentang ciri-ciri balok. Ciri-ciri bangun ruang ini dijabarkan berdasarkan tujuh hal, yaitu sisi, rusuk, titik sudut, diagonal sisi atau diagonal bidang, diagonal ruang, bidang diagonal, dan jaring-jaring. Berikut penjelasan lengkap yang bisa Sedulur simak.
1. Sisi

Telah dijelaskan sebelumnya, balok merupakan bangun ruang yang terdiri atas enam bangun datar berupa persegi panjang. Ciri tersebut membuat balok memiliki enam buah sisi. Sisi bangun ruang ini terdiri atas, alas, depan, belakang, kanan, dan kiri.
Perlu diketahui, keenam sisi bangun ruang ini setidaknya terbagi menjadi tiga pasang yang saling kongruen. Artinya, setiap bagun datar memiliki kesamaan bentuk dan ukuran dengan satu bangun lainnya. Yakni sisi atas kongruen dengan sisi alas, sisi depan kongruen dengan sisi belakang, dan sisi samping kiri kongruen dengan sisi samping kanan.
2. Rusuk balok
Selain memiliki 6 buah sisi, bangun ruang ini juga memiliki 12 rusuk. Rusuk adalah garis yang memotong antara dua sisi bidang atau garis potong antara sisi-sisi balok. Secara sederhana, rusuk dapat dipahami sebagai rangka yang menyusun bangun ruang ini.
Adapun keduabelas rusuk ini terbagi menjadi tiga kategori, yakni 4 rusuk pada sisi atas, 4 rusuk sisi bawah atau alas, dan 4 rusuk sisi tegak.
3. Titik sudut
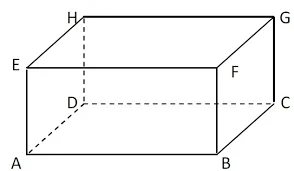
Bangun ruang ini memiliki 8 titik sudut. Titik sudut merupakan titik pertemua tiga rusuk.
Sementara, pada gambar ditunjukkan titik sudut pada bangun ruang tersebut ditandai dengan huruf A, B, C, D, E, F, G, dan H.
4. Diagonal sisi
Diagonal sisi atau juga dikenal sebagai diagonal bidang adalah ruas garis yang menghubungkan dua titik sudut berhadapan pada sebuah sisi balok. Setiap bangun ruang ini memiliki 12 diagonal sisi dengan masing-masing diagonal sisi yang saling berhadapan memiliki ikuran yang sama panjang.
5. Diagonal ruang
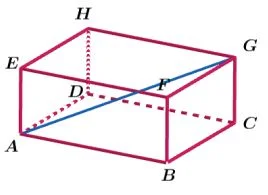
Ciri-ciri balok selanjutnya adalah memiliki 4 buah diagonal ruang. Perlu diketahui, diagonal ruang merupakan ruas garis yang menghubungkan dua titik sudut yang saling berhadapan. Sehingga diagonal ruang saling berpotongan di tengah ruang balok.
6. Bidang diagonal
Bidang diagonal memiliki kemiripan dengan diagonal ruang, yakni berada di tengah ruang bangunan. Hanya saja, bidang diagonal berupa sebuah bidang yang dibatasi oleh dua rusuk dan dua digonal bidang. Setiap balok memiliki 6 bidang diagonal.
7. Jaring-jaring balok
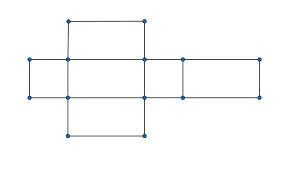
Secara sederhana, jaring-jaring bisa dipahami sebagai kerangka dalam bentuk bidang datar yang apabila digabungkan akan menjadi sebuah bangun ruang. Dengan kata lain, jaring-jaring merupakan wujud datar dari sisi-sisi balok yang direntangkan.
Jaring-jaring balok juga bisa memudahkan Sedulur untuk membuat sebuah bangun ruang balok. Misalnya Sedulur ingin membuat bangun ruang ini dari kertas. Nah, Sedulur bisa memulainya dari membuat jaring-jaring di kertas, kemudian memotongnya dan melipatnya mengikuti garis. Contoh jaring-jaring balok ini juga bisa Sedulur temukan pada kotak kardus makanan yang biasanya dijual dalam bentuk lembaran yang belum dilipat.
BACA JUGA: Rumus Prisma Segitiga Beserta Sifat-Sifat & Contoh Soalnya
Sifat-sifat balok

Berdasarkan ciri-ciri yang sudah diuraikan di atas, bisa disimpulkan sifat-sifat bangun ruang ini sebagai berikut.
- Balok memiliki sisi berbentuk persegi panjang
- Rusuk bangun ruang ini sejajar atau berhadapan memiliki panjang yang sama
- Diagonal bidang sisi yang berhadapan memiliki ukuran yang sama
- Diagonal ruang ukurannya sama panjang
- Bidang diagonalnya berbentuk persegi panjang
Rumus balok
Penting bagi Sedulur untuk mempelajari berbagai rumus dari bangun tiga dimensi ini. Sebab rumus-rumus ini akan berguna untuk mengetahui volume, luas permukaan, hingga keliling.
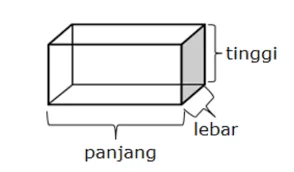
Sebelum masuk ke pembahasan tentang rumus balok, Sedulur perlu tahu elemen-elemen pada bangun ruang ini. Elemen ini berbeda dengan ciri-ciri yang terdiri atas sisi, rusuk, dan lain sebagainya. Apa saja elemen balok?
- Pertama, memiliki panjang atau biasa disimbolkan dengan huruf p. Panjang merupakan rusuk terpanjang dari alas.
- Kedua, adalah lebar atau l yang merupakan rusuk terpendek dari sisi alas.
- Terakhir adalah tinggi atau t. Sesuai namanya, tinggi merujuk pada tinggi balok atau rusuk yang tegak lurus terhadap panjang dan lebar.
Sementara itu, berikut tiga rumus balok yang sudah Super rangkum.
1. Rumus luas permukaan balok
Rumus luas balok adalah 2 ((p x l) + (l x t) + (p x t)).
Jika dijabarkan, rumus ini berasal dari perhitungan luas masing-masing sisi balok. Diketahui, balok memiliki enam buah sisi. Namun harus diingat bahwa ukuran sisi balok tidaklah sama. Sehingga bisa dituliskan:
= (p × l) + (p × t) + (l × t) + (p × l) + (l × t) + (p × t)
= (p × l) + (p × l) + (l × t) + (l × t) + (p × t) + (p × t)
= 2 (p × l) + 2(l × t) + 2(p × t)
= 2 ((p × l) + (l × t) + (p × t)
2. Rumus volume
Volume bangun ruang ini dihitung dengan mengalikan panjang, lebar, dan tinggi. Sehingga bisa dituliskan rumus volume balok adalah sebagai berikut:
Volume = panjang x lebar x tinggi
Volume = p x l x t
3. Rumus keliling
Untuk menghitung keliling sebuah bangun ruang, Sedulur cukup menjumlahkan panjang, lebar, dan tingginya. Namun perlu diketahui, bangun ruang ini tidak hanya memiliki satu rusuk terpanjang, satu rusuk terpendek, maupun satu rusuk yang tegak lurus. Sehingga hasil penjumlahan tersebut perlu dikalikan 4 untuk mendapatkan kelilingnya. Berikut rumusnya.
Keliling = 4 (panjang + lebar + tinggi)
Keliling = 4 (p + l + t)
BACA JUGA: Rumus Luas Permukaan Kubus Beserta Contoh Soalnya
Contoh soal dan pembahasan

Berikut adalah beberapa contoh soal mengenai bangun ruang segi empat ini beserta pembahasannya yang bisa Sedulur pelajari.
Soal 1
Berapa luas permukaan sebuah balok yang memiliki panjang 20 cm, lebar 10 cm, dan tinggi 15 cm?
Jawab =
Untuk menjawab soal di atas, Sedulur bisa menggunakan rumus luas permukaan. Diketahui rumus luas permukaan adalah sebagai berikut.
Luas permukaan (LP) = 2 ((p x l) + (l x t) + (p x t)).
LP = 2 ((20 x 10) + (10 x 15) + (20 x 15))
LP = 2 ((200 + 150 + 300)
LP = 2 (650)
LP = 2 x 650
LP = 1.300 cm2
Perlu diperhatikan, satuan luas adalah centimeter persegi yang ditandai dengan pangkat dua, sebagai berikut “cm2.”
Soal 2
Berapakah volume balok dengan panjang 10 cm, lebar 6cm, dan tinggi 7 cm?
Jawab =
Untuk menjawab soal di atas, Sedulur bisa menggunakan rumus volume. Diketahui rumus volume adalah sebagai berikut.
Volume (Vol) = panjang x lebar x tinggi
Vol = 10 x 6 x 7
Vol = 420 cm3
Perlu diingat, satuan untuk volume adalah centimeter kubik atau cm3.
Soal 3
Seorang anak ingin membuat lampion berbentuk balok dengan ukuran panjang 25 cm, lebar 10 cm, dan tinggi 13 cm. Berapakah panjang kerangka lampion yang harus dibuat?
Jawab =
Perlu diketahui, panjang kerangka sama dengan keliling. Sehingga untuk menghitung panjang kerangka dapat menggunakan rumus keliling sebagai berikut.
Keliling (kel) = 4 (panjang + lebar + tinggi)
Kel = 4 (25 + 10 + 13)
Kel = 4 (48)
Kel = 192 cm
Demikian tadi ulasan mengenai bangun ruang balok beserta contoh soal dan pembahasannya. Semoga artikel ini bisa membantu Sedulur untuk lebih mudah memahami materi ini, ya!



