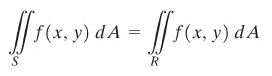Integral adalah salah satu konsep dalam ilmu matematika yang sering disebut sebagai invers dari turunan. Integral banyak digunakan dalam kehidupan sehari-hari, yang mana rumus integral seringkali diterapkan dalam bidang matematika, fisika, dan ekonomi.
Integral termasuk satu diantara tiga konsep ilmu matematika yang saling berkaitan. Dua konsep lainnya adalah limit dan turunan. Hal ini dibuktikan dengan definisi integral yang disebut sebagai kebalikan dari proses turunan atau anti turunan. Berikut adalah penjelasan mengenai rumus integral dan contohnya yang bisa Sedulur simak untuk lebih memahami materi ini.
BACA JUGA: Konsep Bilangan Eksponen Beserta Sifat & Contoh Soalnya
Pengertian

Secara definisi, integral merupakan invers atau kebalikan dari operasi turunan. Integral juga diartikan sebagai lawan dari diferensial, atau lebih dikenal dengan sebutan anti turunan. Integral dikembangkan oleh para ilmuwan matematika dari Yunani bernama Archimedes yang mengemukakan ide tentang integra.
Dalam cabang ilmu matematika, istilah integral biasa digunakan untuk menentukan nilai volume dari sebuah benda putar, luas pada suatu bidang, dan panjang sebuah busur. Tak hanya itu, integral juga biasa digunakan untuk menyelesaikan masalah yang berkaitan dengan populasi, panjang kurva, maupun gaya pada bendungan.
Secara umum, ada dua jenis integral yang dikenal, yakni integral tak tentu dan integral tentu. Integral tak tentu biasanya merujuk pada definisi integral sebagai invers dari turunan, sementara integral tentu merujuk pada jumlahan suatu daerah yang dibatasi kurva atau persamaan tertentu.
Kata integral jika diartikan sebagai kata benda merupakan sebuah fungsi. Sedangkan jika diartikan sebagai kata sifat merupakan “dalam bentuk bilangan bulat”. Misalnya, jika sebuah polinominal memiliki koefisien integral, maka koefisien polinominal semuanya bilangan bulat.
Sementara itu, jika dilihat dari sudut pandang ilmu aljabar, maka integral adalah operasi invers dari operasi turunan. Sedangkan jika dilihat dalam ilmu geometri, integral adalah metode untuk mencari luas daerah limit dari jumlah.
Konsep dasar
Dalam mempelajari integral, Sedulur perlu memahami terlebih dahulu mengenai konsep turunan. Hal ini karena konsep turunan adalah konsep yang digunakan untuk memahami konsep dasar dari integral.
Sebagai cara mudahnya, perhatikan contoh berikut ini.
Jika suatu fungsi memiliki bentuk umum fx= 2×3, maka setiap fungsi memiliki turunan f(x) = 6×2. Jadi, turunan fungsi fx = 2×3 yaitu f(x) = 6×2.
Berdasarkan dari uraian contoh di atas, maka dalam menentukan fungsi f(x) dari fx, sama artinya dengan menentukan anti turunan dari f(x). Berdasarkan definisi dari integral yang merupakan operasi invers dari turunan atau anti diferensial, maka:
Bila f(x) merupakan fungsi umum dengan sifat f’x = fx, maka f(x) merupakan integral dari F’x = f(x). Dalam ilmu matematika, integral biasanya akan dinotasikan sebagai ∫ f(x) = F(x) + C.
Selanjutnya, karena biasanya integral dari f(x) dinotasikan dengan ∫f(x) dx atau “integral f(x) terhadap x”, maka:
Bentuk ∫f(x) dx disebut integral tak tentu dan f(x) di sebut integran. Nah, dari penjelasan tersebut dapat diketahui bahwa ∫axndx = an + 1x n+1 + C (dalam hal ini bilangan rasional dan n ≠ 1).
BACA JUGA: Pengertian Bilangan Bulat Beserta Contoh & Operasi Hitungnya
Rumus integral
Misalkan terdapat suatu fungsi sederhana ax^n. Maka, integral dari fungsi tersebut adalah
Rumus Integral sederhananya:
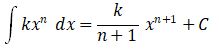
Keterangan:
- k : koefisien
- x : variabel
- n : pangkat/derajat dari variabel
- C : konstanta
Misalkan terdapat suatu fungsi f(x). Jika kita akan menentukan luas daerah yang dibatasi oleh grafik f(x) maka dapat ditentukan dengan
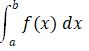
dengan a dan b merupakan gari vertikal atau batas luasan daerah yang dihitung dari sumbu-x. Misalkan integra dari f(x) disimbolkan dengan F(x) atau jika dituliskan
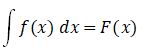
maka
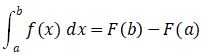
Keterangan:
a, b : batas atas dan batas bawah integral
f(x) : persamaan kurva
F(x) : luasan di bawah kurva f(x)
Sifat integral

Integral memiliki beberapa sifat, yaitu:
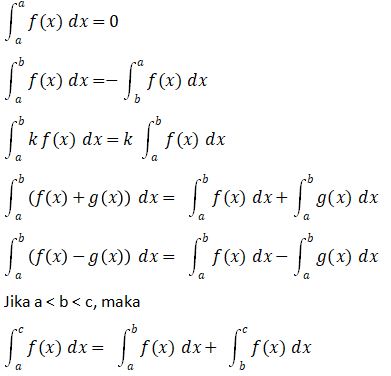
Integral tentu
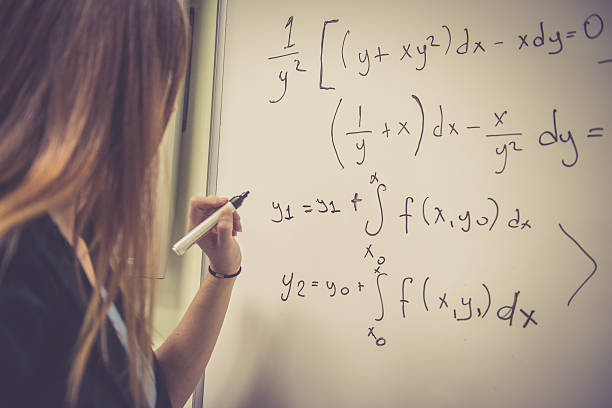
Integral tentu merupakan integral yang memiliki batas. Batas-batas tersebut secara umum merupakan suatu nilai konstanta ataupun variabel. Dalam mencari nilai integral jenis ini, maka Sedulur perlu mensubstitusi batas atas ke fungsi hasil integral yang selanjutnya dikurangi hasil substitusi batas bawah di fungsi hasil integral.
Rumus Integral Tertentu
Rumus integral tentu adalah sebagai berikut:
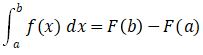
Keterangan:
f(x) = fungsi yang nantinya akan diintegralkan.
F(a) = nilai integral pada batas bawah.
F(b) = nilai integral pada batas atas.
d(x) = variabel integral.
a = batas bawah pada variabel integral.
BACA JUGA: Persamaan Kuadrat dalam Matematika Beserta Contoh Soalnya
Integral Tak Tentu
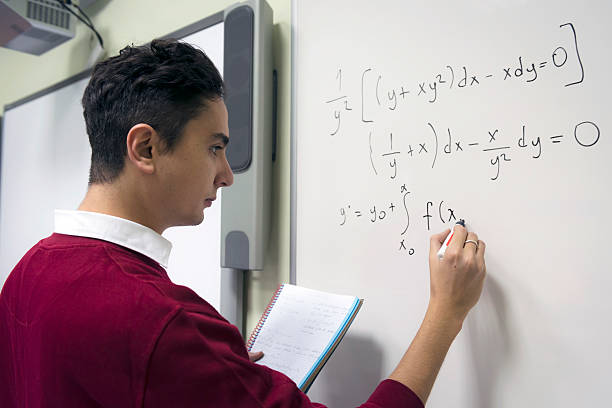
Integral tak tentu merupakan jenis integral yang tidak mempunyai batas. Dalam hal ini, integral tak tentu merupakan suatu proses untuk menentukan bentuk umum dari turunan dari suatu fungsi yang diberikan.
Rumus Integral Tak Tentu
Jika F(x) turunan dari f(x), maka ∫f(x)dx = F(x) + c disebut integral tak tentu, dimana c adalah suatu konstanta sembarang.
Rumus integral tak tentu adalah sebagai berikut:
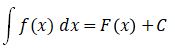
Keterangan:
∫ = lambang integral (operasi anti turunan)
f(x) : persamaan kurva
F(x) : luasan di bawah kurva f(x)
C : konstanta
Integral Pecahan
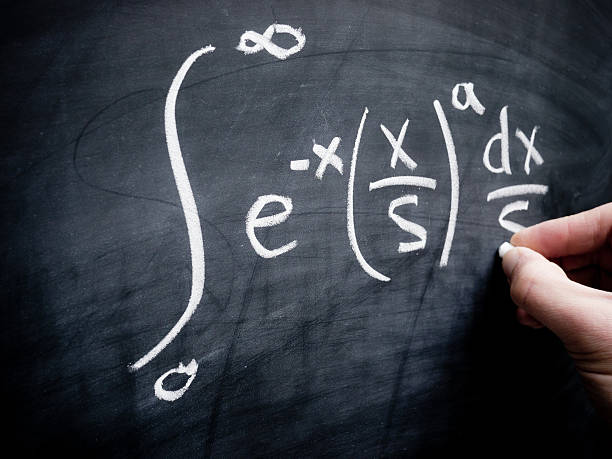
Fungsi pecahan dapat didefinisikan sebagai f(x)/g(x). Penyelesaian integral fungsi pecahan dapat dilakukan dengan memecah fungsi yang kompleks menjadi beberapa fungsi yang lebih sederhana. Perhatikan contoh rumus integral pecahan berikut.
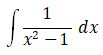
Penyelesaian integral tersebut yaitu sebagai berikut.
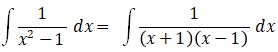
Fungsi pecahan tersebut dapat dipisah menjadi
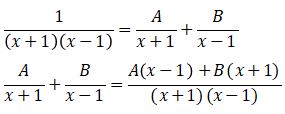
(A + B) x + B – A = 1
Sehingga
B – A = 1 , dan A + B = 0
Didapatkan B = ½ dan A = – ½
Maka, dengan menggunakan sifat integral diperoleh:
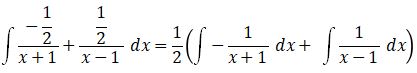
= ½ (- ln |x + 1| + ln |x – 1| + C1)
= – ½ ln |x + 1| + ½ ln |x – 1| + C, dengan C = ½ C1.
Integral Lipat Dua
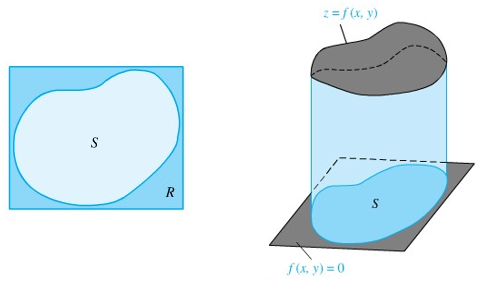
Gambar 1 (Kiri) dan Gambar 2 (kanan)
Integral lipat dua disebut juga integral berulang atau integral ganda merupakan integral untuk fungsi lebih dari dua peubah. Proses pengintegralan yang dilakukan pada integral jenis ini adalah berdasarkan urutan variabelnya. Berikut adalah pembahasan mengenai integral lipat dua untuk daerah yang bukan persegi panjang.
Jika suatu daerah S tertutup dan terbatas pada suatu bidang (seperti terlihat Gambar 1). Daerah S dikelilingi oleh suatu persegi panjang R dengan sisi-sisinya sejajar sumbu-sumbu koordinat (Gambar 1).
Andaikan terdapat suatu fungsi dua peubah f(x,y) yang terdefinisi pada S dan misalkan
f(x,y)=0 pada bagian R di luar S (Gambar 2), maka kita katakan bahwa f dapat diintegralkan pada S jika ia dapat diintegralkan pada R.
Maka rumus integral lipat dua adalah sebagai berikut.
BACA JUGA: Penemu Matematika Beserta Biografi Singkatnya
Integral Substitusi

Beberapa permasalahan atau integral suatu fungsi dapat diselesaikan dengan integral substitusi jika terdapat perkalian fungsi dengan salah satu fungsi merupakan turunan fungsi yang lain.
Perhatikan contoh berikut.
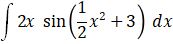
Kita misalkan U = ½ x2 + 3 maka dU/dx = x
Sehingga x dx = dU
Persamaan rumus integral substitusinya menjadi:
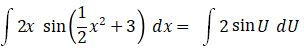
= -2 cos U + C = -2 cos ( ½ x2 + 3) + C
Integral Parsial

Integral parsial biasa digunakan untuk menyelesaikan integral dari perkalian dua fungsi. Secara umum, integral parsial didefinikan dengan teknik penyelesaian persamaan integral dengan pemisalan.
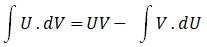
Keterangan:
- U, V : fungsi
- dU, dV : turunan dari fungsi U dan turunan dari fungsi V
Tabel rumus integral trigonometri

Berikut akan disajikan beberapa rumus integral trigonometri dalam tabel.
| Integral fungsi | Hasil integral |
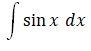 |
-cos x + C |
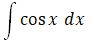 |
sin x + C |
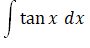 |
ln |sec x| + C |
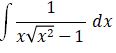 |
arc sec x + C |
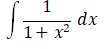 |
arc tan x + C |
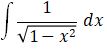 |
arc sin x + C |
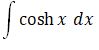 |
sinh x + C |
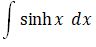 |
cosh x + C |
BACA JUGA: 1 Kodi Berapa Buah? Pengertian & Konversi Satuan Matematika
Contoh soal
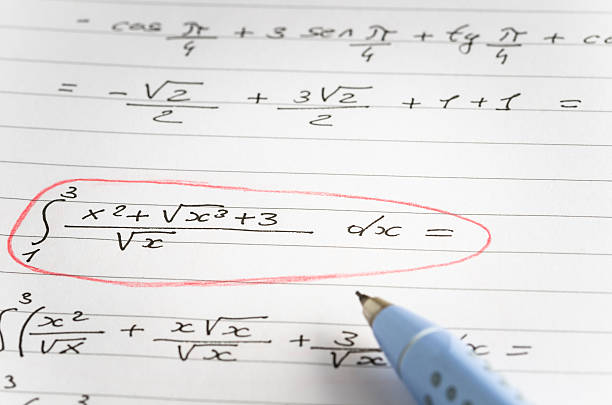
Berikut adalah beberapa contoh soal yang dapat Sedulur pelajari.
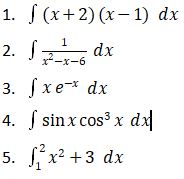
Jawab:
1. 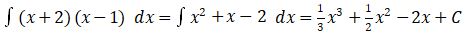
2. 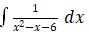
1/(x2 – x + 6) = 1/((x – 3)(x + 2)) = A/(x – 3) + B/(x + 2)
A(x + 2) + B (x – 3) = 1
(A + B) x + 2A – 3B = 1
Diperoleh A = 1/5 dan B = – 1/5
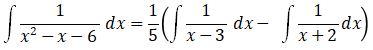
= 1/5 (ln |x – 3| + C1 – ln |x + 2| – C2) = 1/5 ln |x – 3| – 1/5 ln |x + 2| + C, dengan C = 1/5 C1 – 1/5 C2
3. 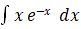 , dapat diselesaikan dengan menggunakan integral parsial.
, dapat diselesaikan dengan menggunakan integral parsial.
Misal:
u = x maka du = dx
dv = ex dx maka v = ![]()
Sehingga,
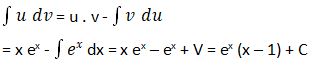
4. 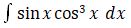
Misal :
u = cos x maka du = – sin x, dengan menggunakan konsep integral substitusi diperoleh:
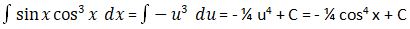
5. 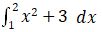
1/3 x3 + 3x + C dengan batas atas 2 dan batas bawah 1, sehingga:
= (1/3 (2)3 + 3 (2)) – (1/3 (1)3 + 3 (1))
= (8/3) + 6 – 1/3 – 3
= 16/3
Penerapan dalam kehidupan sehari-hari

Integral memiliki manfaat yang sangat banyak dalam kehidupan sehari-hari. Kita bisa menggunakan integral dalam berbagai bidang atau disiplin ilmu. Dalam bidang matematika dan teknik, integral dapat digunakan untuk menghitung volume benda putar dan luasan pada kurva.
Sementara itu, pada bidang fisika, integral dapat dimanfaatkan untuk menghitung dan menganalisis rangkaian arus listrik dan medan magnet. Dalam bidang ekonomi, integral juga bisa digunakan untuk menentukan persamaan dan fungsi yang berkaitan dengan ekonomi, konsumsi, marginal, dan lainnya.
1. Menentukan volume benda berputar
Integral dapat dimanfaatkan untuk menentukan volume benda berputar pada beberapa kondisi berikut:
- Menentukan volume benda berputar, yang diputar mengelilingi sumbu X.
- Menentukan volume benda berputar, yang diputar mengelilingi sumbu V.
- Menentukan volume benda berputar yang dibatasi kurva f(x) dan g(x), bila diputar mengelilingi sumbu X.
2. Menentukan luas daerah
Integral dapat dimanfaatkan untuk menentukan luas daerah pada beberapa kondisi berikut:
- Menentukan luas daerah di atas sumbu X.
- Menentukan luas daerah di bawah sumbu X.
- Menentukan luas daerah di antara dua kurva.
- Menentukan luas daerah di atas maupun di bawah sumbu X.
Itulah penjelasan mengenai rumus integral beserta pengertian, sifat, dan contoh soalnya. Semoga informasi ini dapat bermanfaat bagi Sedulur yang sedang belajar mengenai materi kalkulus. Selamat belajar!
Mau belanja bulanan nggak pakai ribet? Aplikasi Super solusinya! Mulai dari sembako hingga kebutuhan rumah tangga tersedia lengkap. Selain harganya murah, Sedulur juga bisa merasakan kemudahan belanja lewat handphone. Nggak perlu keluar rumah, belanjaan pun langsung diantar.
Bagi Sedulur yang punya toko kelontong atau warung, bisa juga lho belanja grosir atau kulakan lewat Aplikasi Super. Harga dijamin lebih murah dan bikin untung makin melimpah.