Apakah Sedulur tahu apa yang dimaksud dengan bilangan eksponen? Secara sederhana, bilangan eksponen diartikan sebagai bilangan berpangkat yang digunakan untuk menulis bentuk perkalian dengan bilangan yang sama secara berulang. Dengan bilangan eksponen, penulisan perkalian maupun suatu bilangan yang rumit dapat diubah menjadi lebih ringkas. Oleh sebab itu masalah bilangan eksponen ini penting untuk dipahami terlebih bagi Sedulur yang duduk di bangku SMA maupun bekerja di bidang yang banyak melakukan hitungan matematika atau fisika.
Ingin tahu bagaimana konsep bilangan eksponen dan sifat-sifatnya? Berikut ini Super telah merangkum informasi selengkapnya. Yuk, langsung kita simak!
BACA JUGA: Bilangan Prima: Pengertian, Cara Menentukan & Contohnya
Pengertian bilangan eksponen

Hal pertama yang perlu Sedulur pahami adalah pengertian bilangan eksponen. Dengan begitu, akan lebih mudah bagi Sedulur untuk memahami lebih jauh tentang materi tersebut.
Pertama, menurut Kamus Besar Bahasa Indonesia (KBBI) Daring, eksponen adalah istilah dalam bidang matematika yang memiliki arti sebagai angka dan sebagainya yang ditulis di sebelah kanan atas angka lain yang menunjukkan pangkat dari angka tersebut. Angka tersebut biasanya ditulis dengan ukuran lebih kecil, misalnya angka 2 pada 2². Bilang eksponen tersebut menunjukkan perkalian angka 2 dengan 2, sehingga ditulis dua pangkat dua (2²).
Sementara itu, dikutip dari Columbia University via Kompas.com, bilangan eksponensial adalah bentuk singkatan matematika yang memungkinkan untuk menulis ekspresi matematika yang rumit menjadi lebih ringkas. Perlu diketahui, bilangan eksponen adalah bilangan yang dikalikan secara berulang-ulang dengan bilangan itu sendiri. Sementara, bilangan eksponensial adalah angka atau huruf yang terletak di sebelah kanan atas ekspresi matematika tertentu atau disebut basis. Adapun bilangan eksponensial juga umum disebut sebagai pangkat.
BACA JUGA: Bilangan Asli: Pengertian, Sifat, Himpunan dan Jenis-Jenisnya
Konsep dan persamaan bilangan eksponen

Telah dipahami bahwa bilangan eksponen adalah bilang berpangkat. Bilangan eksponen sendiri mewakili perkalian antara angka atau bilangan dengan bilangan itu sendiri yang dilakukan secara berulang-ulang.
Bentuk umum persamaan eksponen sendiri dapat dituliskan sebagai berikut.
![]()
Persamaan tersebut menunjukkan a dikali a sebanyak n faktor atau a dikali a secara berulang sebanyak n.
Keteranga:
a^n = a pangkat n
a = bilangan pokok (basis)
n = bilangan eksponensial (pangkat)
Catatan: dalam artikel ini, penulisan bilangan eksponensial atau angka pangkat akan menggunakan lambang “^” sehingga a pangkat n dituliskan sebagai a^n.
BACA JUGA: Rumus Keliling Segitiga: Cara Menghitung Serta Contoh Soalnya
Sifat bilangan eksponen dan contoh soalnya

Setelah memahami pengertian dan bentuk umum atau persamaan eksponen, Sedulur dapat mulai mempelajari sifat-sifat eksponen. Hal ini juga penting untuk dipahami karena akan memudahkan dalam menyelesaikan soal-soal eksponen. Berikut adalah contoh sifat-sifat eksponen beserta dengan soal eksponen yang dapat Sedulur pelajari.
1. Eksponen dengan angka pangkat 1
![]()
Contoh sifat eksponen yang pertama adalah ekspresi matematika dengan bilangan eksponensial 1 atau dipangkatkan 1 memiliki hasil ekspresi matematika itu sendiri. Dengan kata lain, bilangan yang dipangkatkan dengan angka pangkat 1 akan menghasilkan bilangan itu sendiri.
Contoh soal:
1^1 = 1
2^1 = 2
3^1 = 3
100^1 = 100
2. Eksponen dengan angka pangkat nol
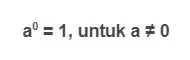
Sifat yang kedua, bilangan eksponen dengan angka pangkat nol (0) akan menghasilkan bilangan 1. Sehingga, bilangan eksponen berapapun basisnya jika memiliki angka pangkat 0, maka akan sama dengan satu. Di sisi lain untuk sifat satu ini, terdapat syarat yaitu a atau basis tidak sama dengan nol. Sebab jika a = 0, hasilnya menjadi tidak terdefinisi.
Contoh soal:
1^0 = 1
2^0 = 1
100^0 = 1
3. Penjumlahan pangkat
![]()
Dalam bilangan eksponen, angka pangkat dapat dijumlahkan dengan angka pangkat lainnya apabila terjadi perkalian antara bilangan eksponen dengan basis yang sama. Misalnya, perkalian antara 2^3 dengan 2^2. Maka dapat dituliskan sebagai berikut.
2^3 x 2^2
= 2^(3+2)
= 2^5
4. Pengurangan pangkat
![]()
Sebelumnya sudah dipahami bahwa perkalian dua bilangan berpangkat atau lebih dengan basis yang sama menghasilkan penjumlahan pangkat. Sebaliknya, jika terjadi pembagian bilangan berpangkat dengan basis sama, maka angka pangkatnya harus dikurangi. Dalam hal ini penting untuk memperhatikan urutan perhitungan bilangan eksponen karena dapat menghasilkan angka pangkat negatif. Contoh pengurangan pangkat pada bilangan berpangkat adalah sebagai berikut.
Contoh soal:
6^9 : 6^3
= 6^(9-3)
= 6^6
5. Perkalian bilangan yang dipangkatkan
![]()
Sifat selanjutnya yaitu perkalian bilangan yang dipangkatkan akan menghasilkan beberapa bilangan dengan pangkat yang sama. Dengan kata lain, masing-masing bilang akan dipangkatkan juga. Untuk lebih memahaminya, perhatikan contoh berikut.
Contoh soal:
(8 x 7)^4
= 8^4 x 7^4
6. Perkalian pangkat
![]()
Dalam materi bilangan berpangkat, Sedulur mungkin juga akan menemukan kasus perkalian pangkat. Umumnya kasus ini dituliskan dengan memangkatkan bilangan berpangkatkan atau (a^m)^n. Jika ditemukan kasus seperti itu, bilangan berpangkat bisa dihitung dengan mengkalikan pangkatnya sehingga bilangan berpangkat dapat ditulis dengan lebih sederhana.
Contoh soal:
(4^2)^3
= 4^(2×3)
= 4^6
7. Pangkat negatif
![]()
atau
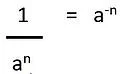
Aturan atau sifat selanjutnya adalah persamaan bilangan eksponen atau bilangan berpangkat dengan pangkat negatif. Jika angka pangkat negatif, maka diubah menjadi pecahan di mana bilangan berpangkat berada di bawah dan menjadi berpangkat negatif. Sebaliknya, bilangan berpangkat positif jika dipindahkan ke bawah akan menjadi negatif.
Contoh soal:
8^-4
= 1 : 8^4
= 1 / 8^4
8. Pembagian bilangan yang dipangkatkan
![]()
atau
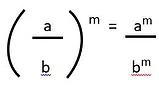
Sifat selanjutnya yaitu pembagian bilangan yang dipangkatkan akan menghasilkan kedua bilangan yang dipangkatkan dengan angka pangkat yang sama. Operasi pembagian di sini juga dapat dituliskan sebagai pecahan. Namun harus diperhatikan bahwa nilai b atau bilangan yang menjadi pembagi atau bilangan penyebut tidak sama dengan nol.
Contoh soal:
(10 : 2)^5 atau (10 / 2)^5
= 10^5 : 2^5 atau 10^5 / 2^5
9. Bilangan berpangkat dengan basis negatif dan pangkat ganjil
![]()
Sifat-sifat bilangan berpangkat lainnya yang harus Sedulur ketahui adalah terkait bilangan berpangkat yang basisnya berupa bilangan negatif. Sifat yang pertama, jika bilangan berpangkat dengan basis negatif memiliki angka pangkat ganjil, maka hasilnya adalah bilangan negatif.
Contoh soal:
(-3)^3
= (-3) x (-3) x (-3)
= -(3 x 3 x 3)
= -27
10. Bilangan berpangkat dengan basis negatif dan pangkat genap
![]()
Sifat yang kedua, jika bilangan berpangkat dengan basis negatif dipangkatkan dengan bilangan genap, maka hasilnya adalah bilangan positif. Berikut contohnya.
(-3)^4
= (-3) x (-3) x (-3) x (-3)
atau juga dapat dituliskan:
= 3^4
= 3 x 3 x 3 x 3
= 81
Demikian tadi pembahasan tentang bilangan eksponen. Dapat dipahami bahwa bilangan eksponen adalah bilangan berpangkat yang digunakan untuk menyederhanakan perkalian antara bilangan yang sama secara berulang. Selain itu juga telah dipaparkan sifat-sifat beserta contoh soal yang dapat membantu Sedulur untuk memahami materi ini. Semoga artikel ini dapat bermanfaat untuk Sedulur, ya!
Mau belanja bulanan nggak pakai ribet? Aplikasi Super solusinya! Mulai dari sembako hingga kebutuhan rumah tangga tersedia lengkap. Selain harganya murah, Sedulur juga bisa merasakan kemudahan belanja lewat handphone. Nggak perlu keluar rumah, belanjaan pun langsung diantar.
Bagi Sedulur yang punya toko kelontong atau warung, bisa juga lho belanja grosir atau kulakan lewat Aplikasi Super. Harga dijamin lebih murah dan bikin untung makin melimpah.



