Determinan Matriks: Pengertian, Cara Menghitung & Contohnya

Saat pelajaran Matematika, Sedulur tentu pernah mendapatkan materi tentang determinan matriks. Definisi dari determinan matriks adalah nilai yang diperoleh dari hasil perhitungan matriks persegi suatu bidang.

Terdapat beberapa rumus mencari determinan, yaitu sarrus dan juga kofaktor. Supaya lebih memahami tentang matriks dan cara menghitungnya, yuk simak penjelasannya berikut ini!

BACA JUGA : Rumus Keliling Segitiga Beserta Pembahasan & Contoh Soalnya

Pengertian determinan matriks

Determinan matriks adalah nilai yang diperoleh dari hasil perhitungan matriks persegi. Matriks persegi yaitu matriks yang mempunyai jumlah yang sama antara baris dan kolom,  sehingga jika digambarkan bentuk matriksnya, akan membentuk bangun layaknya persegi. Nilai determinan disimbolkan dengan “|…|”, misalnya matriks A, nilai determinannya menjadi det A=|A|.

Sedangkan definisi dari determinan invers matriks yaitu invers matriks yang kebalikan (invers) dari sebuah matriks yang ketika matriks tersebut dikalikan dengan inversnya, akan menjadi matriks identitas. Invers matriks dilambangkan dengan A-1. Suatu matriks dapat dikatakan mempunyai invers jika determinan dari matriks tersebut tidak sama dengan nol.

BACA JUGA : Rumus Keliling Lingkaran Beserta Contoh Soal & Pembahasan

Rumus determinan matriks

Berikut cara menentukan determinan matriks ordo 2×2 dan beserta contoh soalnya. 

Determinan matriks 2×2 

Jika,merupakan matriks berordo 2×2. Elemen a dan d terletak pada diagonal utama, sedangkan elemen b dan c terletak pada diagonal kedua. Pada determinan  A dapat dihasilkan dengan mengurangkan hasil kali elemen-elemen diagonal utama dengan hasil kali elemen-elemen pada diagonal kedua. Nah, agar lebih paham tentang materi ini, simak conroh soalnya berikut ini. 

1. Tentukan determinan matriks berikut!

Penyelesaian:

Determinan matriks 3×3

Cara menentukan determinan 3 x 3 terdapat dua cara yaitu cara sarrus dan juga cara minor kofaktor. Agar lebih paham tentang cara menentukan determinan mastriks 3 x 3, yuk simak contoh soalnya berikut ini. 

1. Determinan matriks 3 x 3 sarrus

Tentukan determinan matriks berikut ini menggunakan aturan Sarrus dan metode minor-kofaktor!

Pembahasan:

Untuk mempermudah pengerjaan, tulis kembali elemen-elemen pada kolom ke-1 dan ke-2 di sebelah kanan matriks A sebagai berikut:

Setelah itu, kita tarik garis putus-putus seperti gambar di atas. Kalikan elemen-elemen yang terkena garis putus-putus tersebut. Hasil kali elemen yang terkena garis putus-putus berwarna biru diberi tanda positif (+), sedangkan hasil kali elemen yang terkena garis putus-putus berwarna oranye diberi tanda negatif (-). Ingat urutan penulisannya juga, ya!

Cara ini mungkin terlihat cukup rumit. Namun,jika sudah sering latihan mengerjakan soal, pasti akan hafal dengan sendirinya.

2. Determinan matriks 3×3 kofaktor

Berdasarkan rumus minor-kofaktor, determinan  A dapat dicari dengan cara menghitung jumlah seluruh hasil kali antara kofaktor matriks bagian dari matriks A dengan elemen-elemen pada salah satu baris atau kolom matriks A. Jadi yang pertama dilakukan adalah pilih salah satu baris atau kolom matriks A untuk mendapatkan nilai determinannya. Misalnya, kita pilih baris ke-1. Elemen-elemen matriks baris ke-1, yaitu a₁₁, a₁₂, dan a₁₃.

Kemudian,  karena kita pilih elemen-elemen di baris ke-1, rumus yang kita gunakan adalah sebagai berikut:

Langkah yang kedua, kita harus mencari kofaktor matriks pada bagian matriks A (C_ij). Cij = (-1)^i+j M_ij dan M_ij = det A_ij dengan A_ij merupakan matriks bagian dari matriks A yang diperoleh dengan menghilangkan baris ke-i dan kolom ke-j. 

Sebelumnya, kita telah memilih elemen-elemen pada baris ke-1, yaitu a₁₁, a₁₂, dan a₁₃. Oleh karena itu, matriks bagian dari matriks A nya adalah A₁₁, A₁₂, dan A₁₃.

• A₁₁ diperoleh dengan menghilangkan elemen-elemen pada baris ke-1 dan kolom ke-1.

• A₁₂ diperoleh dengan cara menghilangkan elemen-elemen pada baris ke-1 dan kolom ke-2.

• A₁₃ diperoleh dengan rumus menghilangkan elemen-elemen pada baris ke-1 dan kolom ke-3.

Sehingga akan dihasilkan : 

Cara mencari invers matriks ordo 2 x 2

Tentukanlah invers dari matriks berikut ini!

Pembahasan:

Catatan: elemen-elemen yang berada dalam lingkar biru adalahn diagonal utama matriks A yang ditukar posisinya, sementara itu, elemen-elemen yang berada di lingkar oranye merupakan diagonal kedua matriks A yang dikalikan dengan minus satu (-1). 

Rumus Determinan Matriks 4×4

Untuk dapat menghitung determinan matriks berordo 4×4 kita dapat menggunakan cara sarrus berikut ini:

Determinan Matriks 4×4 Metode Sarrus 

Untuk  bisa mencari determinan dengan ordo 4×4 dengan metode sarrus, diperlukan 4 langkah, berikut adalah langkah penyelesaian dengan penjelasan:

Diketahui: matriks A berordo 4×4

Langkah pertama:
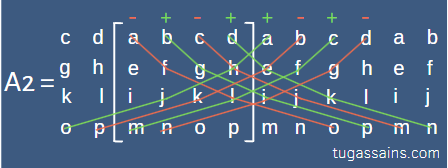
Hitunglah dengan urutan (+ – + – – + – +) dengan jarak 1-1-1

Diperoleh perhitungan:

A1 = afkp – bglm + chin – dejo – ahkn + belo – cfip + dgjm

Langkah kedua:
Hitung menggunakan urutan (- + – + + – + -) dengan jarak 1-2-3

Maka akan diperoleh perhitungan sebagai berikut:

A2 = -aflo + bgip – chjm + dekn + ahjo – bekp + cflm – dgin

Langkah ketiga:
Hitung dengan urutan (+ – + – – + – +) dengan jarak 2-1-2

Diperoleh perhitungan:

A3 = agln – bhio + cejp – dfkm – agjp + bhkm -celn + dfio

Setelah menemukan nilai A1, A2 dan A3, Sedulur bisa langsung menghitung determinan dengan rumus berikut:

Det (A) = A1 + A2 + A3

BACA JUGA : Rumus Luas Belah Ketupat Beserta Contoh & Cara Menghitung

Sifat determinan matriks

Untuk mempermudah dalam mengerjakan soal, Sedulur perlu mengetahui sifat determinan dari matriks, di antaranya yaitu : 

1. Jika semua elemen dari salah satu baris maupun kolom sama dengan nol, maka determinan yang akah dihasilkan adalah nol. 
2. Apabila semua elemen dari salah satu baris atau kolom itu sama dengan elemen-elemen baris atau kolom lain, maka determinan  tersebut adalah nol.
3. Apabila elemen-elemen salah satu dari baris atau kolom adalah kelipatan dari elemen-elemen baris atau kolom lain maka determinannya tersebut adalah nol.

Manfaat mempelajari matriks

Sedulur tentu bertanya-atanya, sebenarnya apa sih manfaat mempelajari matriks? Yuk simak manfaatnya berikut ini:

• Memudahkan untuk membuat analisis tentang suatu masalah ekonomi yang mengandung banyak macam variabel.
• Digunakan untuk memecahkan masalah operasi penyelidikan , misalnya masalah operasi penyelidikan sumber – sumber minyak bumi dan lain sebagainya.
• Dikaitkan dengan penggunaan program linear, analisis input output baik dalam ekonomi, statistika, maupun dalam bidang pendidikan, manajemen, kimia, dan bidang – bidang teknologi yang lainnya.

Itulah penjelasan tentang materi matriks, contoh soal beserta cara penyelesaiannya. Terdapat banyak manfaat mempelajari materi ini diantaraya dapat digunakan untuk memecahkan operasi penyelidikan. Agar lebih mudah dan cepat menyelesaikan soal mengenai determinan, Sedulur harus mengetahui sifat0sifat determinan matriks seperti yang sudah disebutkan di atas. 

Mau belanja bulanan nggak pakai ribet? Aplikasi Super solusinya! Mulai dari sembako hingga kebutuhan rumah tangga tersedia lengkap. Selain harganya murah, Sedulur juga bisa merasakan kemudahan belanja lewat handphone. Nggak perlu keluar rumah, belanjaan pun langsung diantar.

Bagi Sedulur yang punya toko kelontong atau warung, bisa juga lho belanja grosir atau kulakan lewat Aplikasi Super. Harga dijamin lebih murah dan bikin untung makin melimpah.