Rumus Cara Mencari Tinggi Segitiga Beserta Contoh Soalnya

Mencari tinggi segitiga dapat dilakukan dengan beberapa cara. Setidaknya, terdapat 3 cara mencari tinggi segitiga yang diajarkan di sekolah. Cara-cara tersebut dibedakan berdasarkan nilai variabel yang sudah diketahui.

Tinggi segitiga perlu diketahui karena menjadi salah satu variabel untuk mencari luas segitiga. Tanpa tinggi, nilai luas tidak akan bisa ditemukan. Oleh karena itu, mencari nilai tinggi segitiga perlu diketahui untuk menyelesaikan soal-soal matematika mengenai luas segitiga.

Ingin tahu bagaimana cara mencari tinggi segitiga tersebut? Simak informasi selengkapnya berikut ini!

1. Cara mencari tinggi segitiga jika diketahui alas dan luasnya

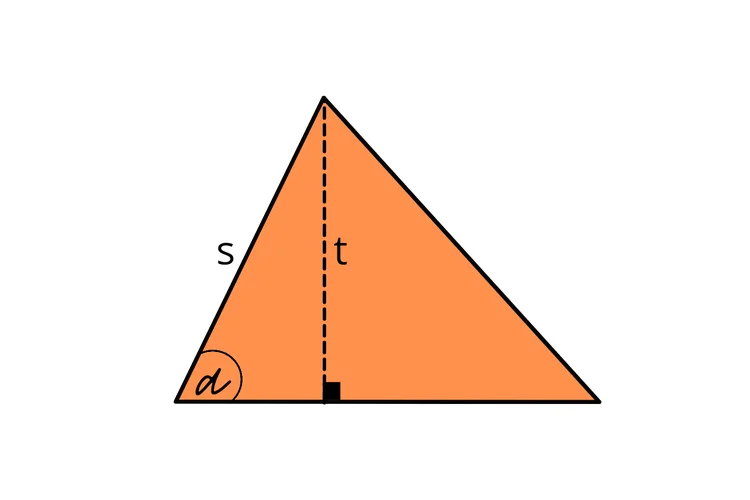
Dalam mencari tinggi segitiga rumusnya bisa berbeda-beda. Hal ini bergantung pada nilai variabel apa yang sudah diketahui. Seperti cara pertama kali ini, kita bisa mencari tinggi segitiga dengan nilai alas dan luas. Berikut adalah caranya:

Perhatikan kembali rumus luas segitiga. Rumus luas segitiga adalah L = ½at. Keterangan: L = luas segitiga, a = panjang alas segitiga, t = tinggi segitiga dari alasnya.
Jika variabel yang diketahui nilainya adalah alas dan luas, maka masukkan nilai luas dalam variabel L. Jika diketahui nilai luas, biasanya soal juga memberikan nilai salah satu sisi sebagai alas. Nah, masukkan nilai alas tersebut sebagai variabel a.
Masukkan nilai yang diketahui ke dalam rumus L = ½at dan hitung. Pertama-tama, kalikan alas (a) dengan ½, kemudian bagi luas (L) dengan hasil perhitungannya. Nilai yang diperoleh adalah tinggi segitiga yang Sedulur cari.

2. Cara mencari tinggi segitiga tanpa diketahui luasnya

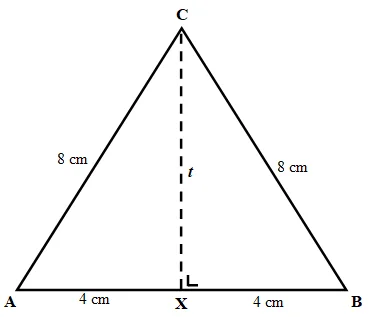
Cara selanjutnya adalah mencari tinggi segitiga tanpa diketahui luasnya. Dalam kasus ini, biasanya soal akan memberitahu nilai variabel yang lain, seperti nilai alas dan sisi miring. Dengan demikian, berikut adalah langkah-langkahnya:

Tentukan variabel yang diketahui. Dalam kasus ini, kita mengetahui nilai alas dan sisi miring. Letakkan alas sebagai variabel a dan sisi miring sebagai variabel s.
Gunakan teorema Phytagoras untuk mengetahui tinggi segitiga. Hal ini karena alas, sisi miring, dan tinggi segitiga dapat membentuk segitiga siku-siku yang memenuhi persamaan Phytagoras.
Nilai sisi miring merupakan nilai tinggi ditambah alas, dengan demikian dapat dituliskan, s² = t² + (½ x a)².
Karena yang dicari adalah nilai tinggi segitiga, maka rumus dapat dibalik menjadi, t² = s² – (½ x a)².
Nilai tinggi dapat diperoleh dengan mencari akar kuadrat dari hasil rumus, jadi t = s² – (½ x a)² .

3. Cara mencari tinggi segitiga jika diketahui kelilingnya

Cara selanjutnya bisa dilakukan jika tinggi yang dicari adalah segitiga sama sisi. Jika diketahui nilai kelilingnya, maka nilai sisinya adalah k/3 karena segitiga sama sisi memiliki nilai sisi yang sama. Berikut adalah langkahnya:

Bagi nilai keliling dengan jumlah sisi. Karena segitiga memiliki jumlah sisi 3, maka bagi nilai keliling dengan angka 3.
Setelah diketahui nilai sisinya, ingatlah bahwa segitiga sama sisi memiliki 3 sisi yang sama panjang dan tiga sudut yang sama besar, yakni masing-masing 60 derajat. Jika segitiga sama sisi dibagi menjadi dua bagian sama besar, maka hasilnya adalah dua segitiga siku-siku yang kongruen.
Setelah mendapatkan bentuk segitiga siku-siku, ingat kembali mengenai Teorema Pythagoras. Teorema ini menyatakan bahwa untuk semua segitiga siku-siku dengan panjang sisi a dan b serta sisi miring c, maka akan berlaku rumus a² + b² = c². Nah, gunakan rumus pada teorema ini untuk mencari tinggi segitiga sama sisi.
Selanjutnya, bagi segitiga sama sisi menjadi dua bagian sama besar, dan tandai sisi-sisinya sebagai variabel a, b, dan c. Sisi miring c akan memiliki panjang sama dengan panjang sisi segitiga sama sisi. Sisi a akan memiliki panjang sama dengan ½ panjang sisi sebelumnya, dan sisi b adalah tinggi segitiga yang harus dicari.
Masukkan nilai panjang tersebut ke dalam Teorema Pythagoras untuk mencari nilai b². Caranya, kuadratkan c dan a dengan mengalikan masing-masing angka dengan angka yang sama. Lalu, kurangi a² dari c². Jadi b² = c² – a².
Selanjutnya cari akar kuadrat dari b² untuk mengetahui nilai tinggi segitiga. Jadi, b = c²-a² .

4. Cara mencari tinggi macam-macam segitiga

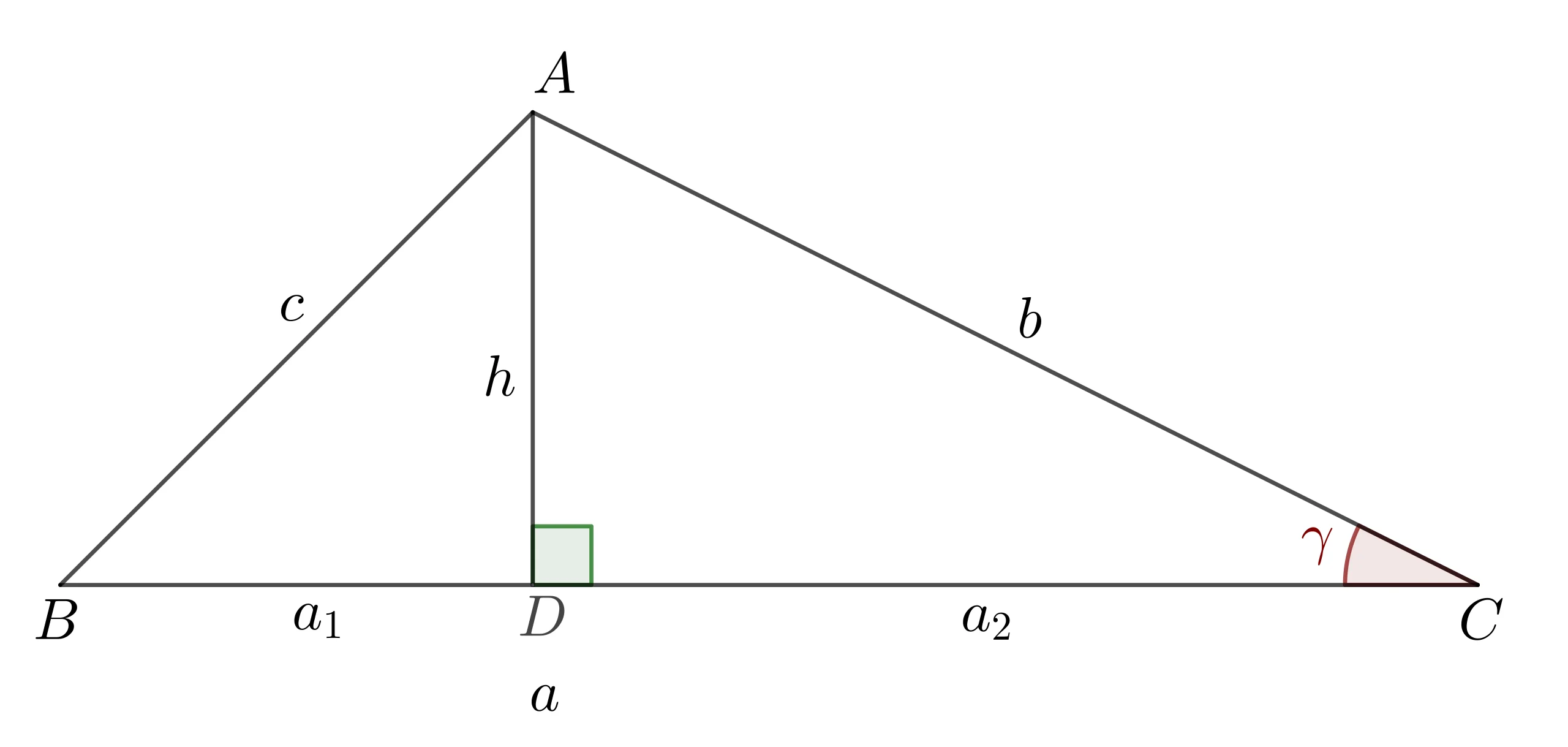
Jika Sedulur ingin mengetahui cara lainnya, maka berikut adalah cara-cara mencari tinggi segitiga sesuai dengan jenisnya.

Cara mencari tinggi segitiga siku-siku

Rumus: a² + b² = c²

b² = c² – a²

b = c²-a²

Cara mencari tinggi segitiga sama kaki

Rumus: t² = s² – ½a²

Cara mencari tinggi segitiga sembarang

Rumus: t = 2L/a

Cara mencari tinggi segitiga sama sisi

Rumus: t = ½ a√3

Contoh soal

Sebuah segitiga memiliki alas sebesar 5 cm dan luas sebesar 15 cm². Berapakah nilai tinggi segitiga tersebut?

Jawab:

Diketahui: a = 5 cm

L = 15 cm²

Ditanya:

t = ?

Dijawab:

Karena tidak diketahui jenis segitiganya, maka kita dapat mencari tinggi segitiga dengan rumus segitiga sembarang.

t = 2L/a

t = (2 x Luas Δ ) : a

t = (2 x 15) : 5

t = 6

Jadi, segitiga sembarang tersebut memiliki tinggi 6 cm.

Jika diketahui sebuah segitiga sama sisi memiliki panjang sisi 8 cm. Tentukanlah tinggi segitiga tersebut!

Jawab:

Diketahui:

s = 8 cm

Ditanya:

t = ?

Dijawab:

Sedulur dapat menggunakan teorema phytagoras dengan cara:

b² = c² – a²

b² = 8² – 4²

b² = 64 – 16

b² = 48

b = √48

b = 4√3

Sedulur juga dapat menggunakan rumus yang lebih cepat, yakni

t = ½ a√3

t = ½ (8 cm)√3

t = 4√3

Jadi, nilai tinggi segitiga sama sisi tersebut adalah 4√3 cm.

Diketahui sebuah segitiga siku-siku memiliki ukuran sisi miring 15 cm dan alas 9 cm. Tentukan nilai tinggi segitiga siku-siku tersebut!

Jawab:

Diketahui:

s = 15 cm

a = 9 cm

Ditanya:

t = ?

Dijawab:

b = c²-a²

b = 15²-9²

b = 225-81

b = 144

b = 12 cm

Jadi, tinggi segitiga siku-siku tersebut adalah 12 cm.

Nah, itulah informasi mengenai rumus cara mencari tinggi segitiga beserta contoh soalnya. Semoga informasi ini dapat bermanfaat dan menambah wawasan Sedulur dalam mempelajari ilmu matematika terkhusus pada bab segitiga. Selamat belajar!

Mau belanja bulanan nggak pakai ribet? Aplikasi Super solusinya! Mulai dari sembako hingga kebutuhan rumah tangga tersedia lengkap. Selain harganya murah, Sedulur juga bisa merasakan kemudahan belanja lewat handphone. Nggak perlu keluar rumah, belanjaan pun langsung diantar.

Bagi Sedulur yang punya toko kelontong atau warung, bisa juga lho belanja grosir atau kulakan lewat Aplikasi Super. Harga dijamin lebih murah dan bikin untung makin melimpah.