Trigonometri merupakan salah satu cabang dalam ilmu matematika. Secara sederhana, trigonometri mempelajari tentang hubungan sudut dan panjang segitiga. Di samping itu, dalam materi trigonometri juga dipelajari tentang turunan trigonometri. Yaitu proses matematis yang digunakan untuk menentukan turunan suatu fungsi trigonometri.
Ingin tahu lebih jauh mengenai turunan trigonometri? Berikut Super telah merangkum informasi selengkapnya.
BACA JUGA: Persamaan Kuadrat dalam Matematika Beserta Contoh Soalnya
Mengenal fungsi trigonometri

Sebelum masuk ke pembahasan tentang turunan trigonometri, tidak ada salahnya Sedulur memahami terlebih dahulu mengenai pengertian trigonometri. Menurut Kamus Besar Bahasa Indonesia (KBBI), trigonometri adalah ilmu ukur mengenai sudut dan sempadan segitiga. Di sisi lain, kata trigonometri berasal dari kata dalam bahasa Yunani, yakni “trigono” yang berarti tiga sudut dan “metron” yang artinya mengukur. Berdasarkan pengertian itu dapat dijelaskan bahwa trigonometri adalah cabang matematika yang mempelajari hubungan yang meliputi panjang dan sudut segitiga.
Dirangkum dari berbagai sumber, ilmu trigonometri pertama kali muncul pada masa Helenistik pada abad ke-3 sebelum Masehi (SM). Bidang trigonometri ini muncul dari penggunaan geometri untuk mempelajari astronomi.
Definisi turunan trigonometri

Turunan trigonometri dikenal sebagai diferensiasi trigonometri atau diferensial trigonometri. Sementara itu, definisi turunan trigonometri bisa dijelaskan sebagai proses matematis untuk menentukan turunan dari suatu fungsi trigonometri atau tingkat perubahan terkait dengan suatu variabelnya.
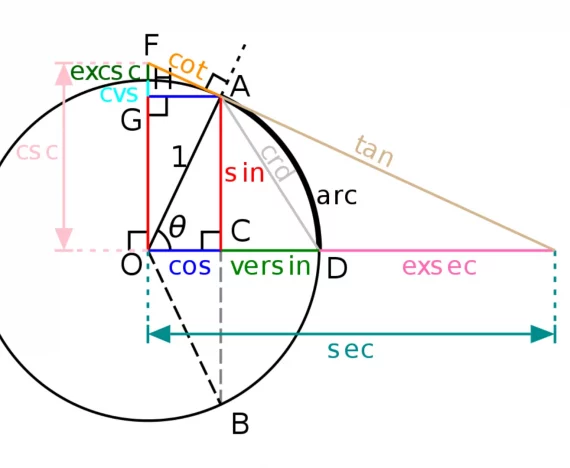
Untuk memahami masalah trigonometri maupun turunan trigonometri, Sedulur perlu mengetahui fungsi trigonometri. Secara umum, ada 6 fungsi yaitu sebagai berikut.
- Sinus atau sin
- Cosinus atau cos
- Tangen atau tan
- Cotangen atau cot
- Secant atau sec
- Cosecant atau csc
Contoh turunan fungsi trigonometri
Untuk lebih memahami mengenai turunan dari fungsi trigonometri, Sedulur bisa melihat contoh berikut.
Misalnya diketahui fungsi:
f(x) = sin(x)
Maka, turunan dari fungsi tersebut dapat dituliskan sebagai berikut.
f'(a) = cos(a)
Perlu diketahui, f'(a) adalah tingkat perubahan sin(x) di titik a. Adapun f’ yang dibaca sebagai f aksen adalah suatu fungsi baru.
BACA JUGA: Logaritma: Pengertian, Sifat, Fungsi, Rumus & Persamaannya
Rumus
Rumus turunan trigonometri digunakan untuk mengetahui tingkat perubahan yang berkaitan dengan suatu variabelnya. Berikut adalah 6 rumusnya.
- Turunan dari f(x) = sin x adalah f'(x) = cos x
- Turunan dari f(x) = cos x adalah f'(x) = −sin x
- Turunan dari f(x) = tan x adalah f'(x) = sec2 x
- Turunan dari f(x) = cot x adalah f'(x) = −csc2 x
- Turunan dari f(x) = sec x adalah f'(x) = sec x . tan x
- Turunan dari f(x) = csc x adalah f'(x) = −csc x . cot x
Rumus perluasan turunan fungsi trigonometri
Selanjutnya, Sedulur perlu mengetahui mengenai rumus perluasan dalam turunan fungsi trigonometri. Rumus perluasan ini digunakan apabila ditemukan kondisi tertentu yang tidak bisa diselesaikan dengan rumus dasar.
Rumus perluasan I
- Turunan dari f(x) = sin u adalah f'(x) = cos u . u’
- Turunan dari f(x) = cos u adalah f'(x) = −sin u . u’
- Turunan dari f(x) = tan u adalah f'(x) = sec2u . u’
- Turunan dari f(x) = cot u adalah f'(x) = −csc2 u . u’
- Turunan dari f(x) = sec u adalah f'(x) = sec u tan u . u’
- Turunan dari f(x) = csc u adalah f'(x) = −csc u cot u . u’
Rumus perluasan II
- Turunan dari f(x) = sin (ax + b) adalah f'(x) = a cos (ax + b)
- Turunan dari f(x) = cos (ax + b) adalah f'(x) = -a sin (ax + b)
- Turunan dari f(x) = tan (ax + b) adalah f'(x) = a sec2 (ax + b)
- Turunan dari f(x) = cot (ax + b) adalah f'(x) = -a csc2 (ax + b)
- Turunan dari f(x) = sec (ax + b) adalah f'(x) = a tan (ax + b) . sec (ax + b)
- Turunan dari f(x) = csc (ax + b) adalah f'(x) = -a cot (ax + b) . csc (ax + b)
BACA JUGA: Bilangan Asli: Pengertian, Sifat, Himpunan dan Jenis-jenisnya
Contoh soal dan pembahasan

Soal 1
Tentukan turunan dari y = -2 cos x
Jawaban:
Misal, f(x) = cos x adalah f'(x) = −sin x
Maka, penyelesaian untuk turunan y = -2 cos x adalah
y = -2 cos x
y’ = -2 (-sin x)
y’ = 2 sin x
Soal 2
Tentukan turunan y = sin 3x
Jawaban
Misal, u = 3x ⇒ u’ = 3
Maka, penyelesaian untuk turunan y = sin 3x adalah
y = sin 3x
y’ = cos u . u’
y’ = cos 3x . 3
y’ = 3cos 3x
Soal 3
Tentukan turunan y = cosx2
Jawaban
Misal, turunan u = x2 adalah u’ = 2x
Maka, penyelesaian untuk turunan y = cosx2 adalah
y = cos u
y’ = -sin u . u’
y’ = -sin x2 . 2x
y’ = -2x sin x2
BACA JUGA: Memahami Rumus Pythagoras Beserta Contoh Soalnya
Trivia

Fungsi invers
Secara sederhana, fungsi invers adalah fungsi kebalikan. Sehingga dapat dijelaskan bahwa fungsi invers adalah fungsi yang merupakan kebalikan dari suatu fungsi. Dalam kaitannya dengan trigonometri, fungsi invers trigonometri adalah fungsi invers dari suatu fungsi sinus, cosinus, tangen, cotangen, secan, dan cosecan.
Fungsi hiperbolik
Fungsi hiperbolik merupakan hasil kombinasi dari fungsi-fungsi eksponen. Untuk diketahui, eksponensial adalah operasi matematika yang dilambangkan dengan b pangkat n. Yaitu operasi matematika yang melibatkan dua bilangan b dan eksponen atau pangkat n. Terkait dengan turunan fungsi trigonometri, mungkin Sedulur pernah mendengar istilah turunan trigonometri invers, turunan trigonometri hiperbolik, dan turunan trigonometri berpangkat. Nah, materi-materi tersebut akan dibahas di artikel berikutnya, ya.
Demikian tadi pembahasan mengenai turunan fungsi trigonometri. Semoga artikel ini dapat membantu Sedulur untuk lebih memahami masalah trigonometri khususnya turunan trigonometri, ya!
Mau belanja bulanan nggak pakai ribet? Aplikasi Super solusinya! Mulai dari sembako hingga kebutuhan rumah tangga tersedia lengkap. Selain harganya murah, Sedulur juga bisa merasakan kemudahan belanja lewat handphone. Nggak perlu keluar rumah, belanjaan pun langsung diantar.
Bagi Sedulur yang punya toko kelontong atau warung, bisa juga lho belanja grosir atau kulakan lewat Aplikasi Super. Harga dijamin lebih murah dan bikin untung makin melimpah.



