Rumus torsi adalah rumus yang digunakan untuk menghitung besaran vektor yang bekerja sehingga sebuah benda melakukan gerakan rotasi. Dalam ilmu fisika, istilah torsi juga kerap disebut sebagai momen gaya dan didefinisikan sebagai gaya eksternal yang menyebabkan benda berputar. Torsi atau momen gaya disimbolkan dengan huruf Yunani “τ” dan memiliki satuan Newton meter atau Nm.
Nah, agar Sedulur lebih memahami materi ini, berikut Super telah merangkum informasi lengkapnya mulai dari pengertian, contoh soal, dan pembahasannya. Yuk, langsung disimak!
BACA JUGA: Rumus Simpangan Rata Rata Beserta Pengertian & Contohnya
Apa itu torsi?

Sebelum masuk ke pembahasan yang lebih jauh, ada baiknya Sedulur memahami pengertian torsi terlebih dahulu. Dengan begitu, akan lebih mudah bagi Sedulur untuk mempelajari materi satu ini.
Seperti yang telah disinggung sebelumnya, torsi atau momen gaya dipelajari dalam bidang fisika. Pemahaman tentang materi ini diperlukan untuk mempelajari masalah dinamika rotasi, yaitu ilmu mengenai gerak rotasi dengan memperhatikan aspek penyebabnya.
Sementara mengutip dari Modul Fisika Kelas XI pada laman Kemdikbud, torsi adalah besaran vektor yang menyebabkan terjadinya percepatan sudut sehingga sebuah benda dapat berotasi atau berputar. Misalnya ketika Sedulur memutar baut menggunakan kunci. Pada kegiatan tersebut, Sedulur memberikan gaya kepada kunci tersebut sehingga terjadi gerakan rotasi yang sekaligus akan memutar baut.
Adapun besaran vektor sendiri merupakan besaran yang memiliki besar dan arah. sebagai besaran vektor, torsi dapat memiliki dua arah, yaitu searah dan berlawanan arah jarum jam. Umumnya, torsi akan memiliki nilai positif apabila benda berputar berlawanan dengan arah jarum jam. Sebaliknya, jika arah putarannya searah dengan arah jarum jam, torsi akan bernilai negatif.
BACA JUGA: Cara Menghitung Skala Peta Beserta Rumus & Contoh Soalnya
Rumus torsi
Setelah memahami pengertian torsi atau momen gaya, Sedulur tentu ingin tahu bagaimana cara menghitungnya. Secara umum, torsi dapat diperoleh dengan menghitung vektor gaya dikalikan jarak vektor. Dengan kata lain, rumus torsi ialah besar gaya (F) dikalikan dengan panjang lengan gaya (r). Untuk lebih jelasnya, berikut persamaan rumus torsi atau rumus momen gaya.
τ = r × F
Keterangan:
- τ adalah torsi atau momen gaya, memiliki satuan Newton meter (Nm)
- r adalah lengan gaya, lengan momen, jarak titik poros dengan gaya, atau juga disebut jarak vektor, memiliki satuan meter (m)
- F adalah gaya yang bekerja, memiliki satuan Newton (N)
Rumus di atas dapat digunakan apabila gaya yang bekerja tegak lurus dengan lengan gaya. Sementara, apabila gaya yang bekerja tidak tegak lurus terhadap lengan gaya, Sedulur bisa menggunakan persamaan berikut.
τ = r x F x sinθ
Keterangan:
- τ adalah torsi atau momen gaya, memiliki satuan Newton meter (Nm)
- r adalah lengan gaya atau lengan momen, memiliki satuan meter (m)
- F adalah gaya yang bekerja, memiliki satuan Newton (N)
- θ adalah sudut yang terbentuk antara garis gaya yang bekerja (F) terhadap lengan gaya (r)
BACA JUGA: Energi Potensial adalah: Pengertian, Jenis dan Rumusnya
Contoh soal dan pembahasan

Untuk lebih memahami materi ini, Sedulur dapat menyimak beberapa contoh soal yang juga dilengkapi dengan penyelesaiannya berikut ini.
Contoh 1
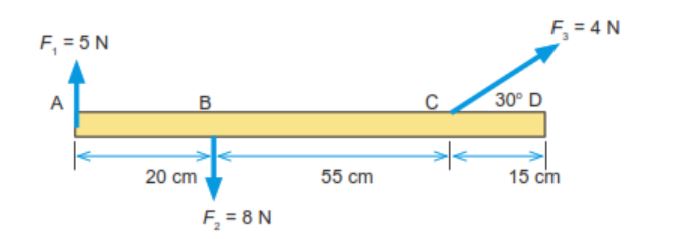
Tiga buah gaya bekerja pada batang AD seperti pada gambar. Diketahui batang AD memiliki massa 2 kg dengan g = 10 m/s². Hitunglah berada resultan momen gaya terhadap titik B pada batang tersebut!
Penyelesaian:
Pertama, diketahui vektor-vektor gaya yang bekerja pada batang AD meliputi F1 = 5N, F2 = 8N, dan F3 = 4N. Selain itu dapat dituliskan jarak vektor atau r dari titik E (tepat di tengah batang) ke B adalah 25 cm. Sehingga momen gaya pada batang tersebut dapat dihitung menggunakan rumus sebagai berikut.
τB = τBA + τBE + τBC
τB = -(rBA x F1) + -(rBE x w) + (rBC x F3 x sin 30)
τB = -(0,2 x 5) – (0,25 x 2 x 10) + (0,55 x 4 x 0,5)
τB = -1 – 5 + 1,1
τB = -6 + 1,1
τB = -4,9 Nm
Maka, resultan momen gaya terhadap poros B adalah 4,9 Nm. Adapun tanda minus atau negatif (-) menunjukkan bahwa resultan momen gaya searah putaran jarum jam.
(Sumber soal: Modul Fisika Kelas XI – Kemdikbud)
Contoh 2
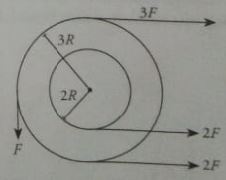
Sebuah sistem dua roda seporos bebas berotasi terhadap sumbu tanpa gesekan melalui pusat bersama roda dan tegak lurus terhadap bidang kertas. Pada roda tersebut bekerja empat gaya dalam arah tangensial terhadap tepi-tepi roda seperti yang ditunjukkan pada gambar. Hitung besar momen resultan pada sistem tersebut!
Penyelesaian:
Pertama, diketahui titik poros terletak di pusat lingkaran dan terdapat empat gaya yang bekerja. Sehingga dapat diuraikan gaya dan jarak dari porsnya sebagai berikut:
Gaya 1 : 3F, 3R, searah jarum jam
Gaya 2 : F, 3R, berlawanan arah jarum jam
Gaya 3 : 2F, 2R, berlawanan arah jarum jam
Gaya 4 : 2F, 3R, berlawanan arah jarum jam
Berdasarkan data di atas, dapat dihitung momen gaya atau momen resultannya sebagai berikut.
τ = τ1 + τ2 + τ3 + τ4
τ = -(3F x 3R) + F x 3R + 2F x 2R + 2F x 3R
τ = -9FR + 3FR + 4FR + 6FR
τ = 4FR
Maka, nilai momen resultan gaya pada sistem dua roda di atas adalah 4FR.
(Sumber soal: Zenius)
BACA JUGA: Pengertian Suhu Beserta Rumus, Alat Ukur, Skala & Satuannya
Contoh 3
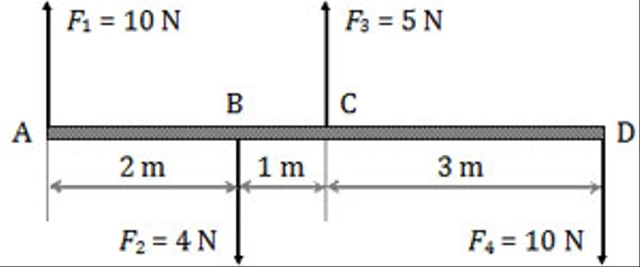
Pada batang ABCD bekerja gaya F1, F2, F3, dan F4 seperti ditunjukkan pada gambar. Jika massa batang diabaikan, maka berapa nilai momen gaya terhadap titik atau poros A?
Penyelesaian:
Pada rotasi benda terhadap suatu poros, gaya yang bekerja pada poros tersebut tidak berfungsi. Sehingga pada perhitungan momen gaya terhadap poros A, F1 akan mati atau tidak berfungsi.
Adapun F2, F3, dan F4 berperan pada rotasi batang dengan pusat titik A. F2 dan F4 bekerja searah jarum jam sehingga memiliki nilai negatif, sedangkan F3 berlawanan arah jarum jam dan memiliki nilai positif. Berikut uraian perhitungannya.
τA = τAB + τAC + τAD
τA = -(rAB x F2) + (rAC x F3) + -(rAD x F4)
τA = -(2 x 4) + (3 x 5) + -(6 x 10)
τA = -8 + 15 – 60
τA = -53 Nm
Maka diketahui bahwa resultan momen gaya terhadap titik A adalah 53 Nm. Tanda negatif di sini menunjukkan lebih besar momen gaya yang searah putaran jarum jam.
(Sumber soal: Kumparan)
Contoh 4
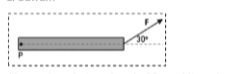
Gaya 16 N bekerja pada sebuah batang dengan panjang 25 cm seperti ditunjukkan pada gambar. Hitung berapa momen gaya terhadap titik P!
Penyelesaian:
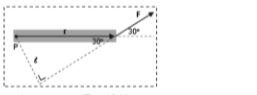
Diketahui gaya atau F pada batang adalah 16 N. Sementara besar vektor posisi atau jarak titik poros dengan gaya (r) adalah 25 cm = 0,25 m. Perlu diperhatikan pula bahwa gaya tidak tegak lurus terhadap benda, sehingga digunakan rumus τ = r x F x sinθ di mana besar sudut adalah 30 derajat.
Berikut hitungan momen gaya pada batang tersebut.
τ = r x F x sinθ
τ = 0,25 x 16 x sin 30
τ = 0,25 x 16 x 0,5
τ = 3 Nm
Maka, besar momen gaya terhadap poros P adalah 2 Nm.
(Sumber soal: Detik)
Demikian tadi pembahasan mengenai rumus torsi atau momen gaya. Pada artikel di atas juga telah diuraikan contoh soal mengenai momen gaya beserta pembahasannya. Semoga informasi ini bisa menambah wawasan Sedulur, ya!
Mau belanja bulanan nggak pakai ribet? Aplikasi Super solusinya! Mulai dari sembako hingga kebutuhan rumah tangga tersedia lengkap. Selain harganya murah, Sedulur juga bisa merasakan kemudahan belanja lewat handphone. Nggak perlu keluar rumah, belanjaan pun langsung diantar.
Bagi Sedulur yang punya toko kelontong atau warung, bisa juga lho belanja grosir atau kulakan lewat Aplikasi Super. Harga dijamin lebih murah dan bikin untung makin melimpah.



