Tabel kebenaran dibutuhkan untuk mengetahui nilai kebenaran dari sebuah premis atau sebuah pernyataan. Nilai kebenaran dari sebuah pernyataan atau premis merupakan klasifikasi yang terdiri dari dua kemungkinan yaitu Benar atau Salah.
Klasifikasi tersebut dinotasikan dalam bentuk B atau S. Selain itu, tabel kebenaran juga berfungsi untuk memberikan informasi terkait argumen yang valid dan tidak valid. Bagi Sedulur yang belum tahu cara membuat tabel kebenaran, yuk kita simak langkahnya di bawah ini!
BACA JUGA: Memahami Rumus Persamaan Lingkaran dan Contoh Soalnya
Cara membuat tabel kebenaran

Di awal telah disinggung bahwa tujuannya adalah untuk mengukur sebuah nilai kebenaran dari sebuah premis atau pernyataan. Tabel ini berkaitan dengan pelajaran logika matematika yang diajarkan untuk tingkat SMA (Sekolah Menengan Atas).
Adapun untuk membuat tabel kebenaran langkah yang dibutuhkan adalah sebagai berikut:
- Isilah kolom pertama dengan huruf B sebanyak 2^n-1 (dibaca dua pangkat n minus 1), mulai dari baris pertama berurut ke bawah. Kemudian, diikuti dengan huruf S sebanyak 2^n-1 berturut-turut pula ke bawah.
- Isilah kolom kedua mulai dari baris pertama dengan huruf B sebanyak 2^n-2 berturut-turut, diikuti dengan huruf S sebanyak 2^n-1 pula. Untuk baris setelahnya yang masih kosong diisi dengan pola huruf B dan S yang telah ada sebelumnya, sampai semua baris terisi.
- Isilah kolom ketiga mulai baris pertama dengan huruf B sebanyak 2^n-3, dilanjutkan dengan huruf S sebanyak 2^n-3 pula. Demikian seterusnya untuk baris-baris setelahnya, diisi sama dengan pola B dan S yang telah ada sebelumnya.
Simbol kurang lebih (±) atau plus minus menunjukkan dua kemungkinan nilai, kurang dari angka yang ditunjukkan atau lebih dari itu. Misalnya, ±100 maka kemungkinan bisa kurang dari 100 atau lebih dari 100. Simbol ini lebih sering digunakan ketika mengacu pada angka atau berat.
Dalam tabel juga akan sering ditemui simbol-simbol yang menjelaskan akan suatu hal. Khusus berkaitan tabel ini, akan dijelaskan dalam penjelasan selanjutnya.
Kolom pernyataan majemuk

Dari cara membuat tabel kebenaran di atas, Sedulur bisa terus mengisi kolom pernyataan tunggal terisi. Setelah kolong pernyataan majemuk, dilanjut dengan mengisi kolom pernyataan majemuk. Kolom pernyataan majemuk adalah pernyataan gabungan.
Pernyataan gabungan dari beberapa pernyataan tunggal yang dihubungkan dengan kata hubung. Pernyataan majemuk tersebut dapat dibagi menjadi empat, yaitu konjungsi, disjungsi, implikasi dan biimplikasi. Berikut penjelasan lebih lengkapnya:
1. Konjungsi (∧)
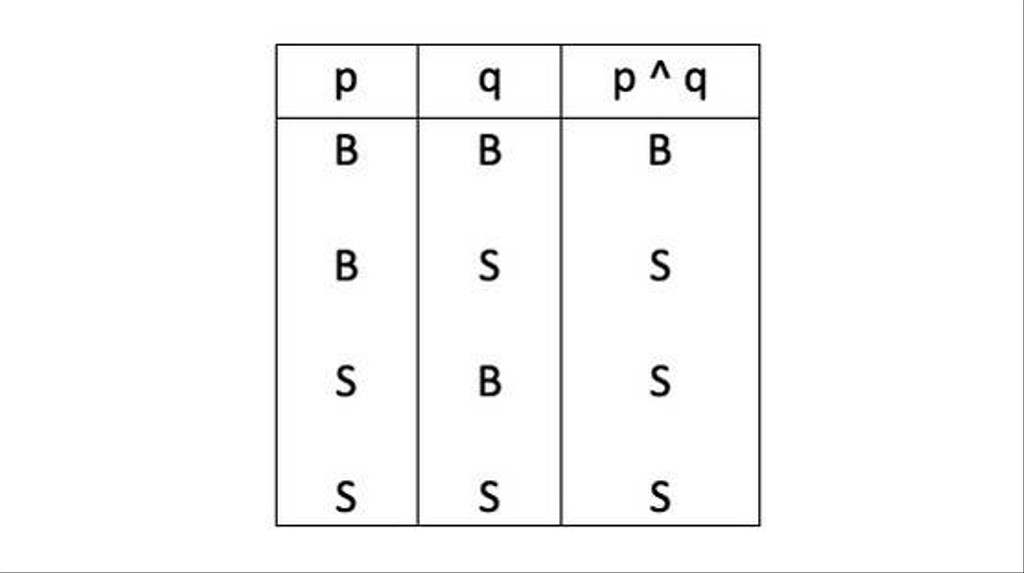
Konjungsi adalah pernyataan majemuk yang menggunakan kata hubung ‘dan’. Bentuk notasinya adalah “p ∧ q” yang dibaca “p dan q”. Sebagaimana yang dapat Sedulur lihat dalam tabel di atas. Adapun keterangannya adalah sebagai berikut:
- p = pernyataan 1
- q = pernyataan 2
- p ^ q = p dan q
- B = benar
- S = salah
2. Disjungsi (∨)
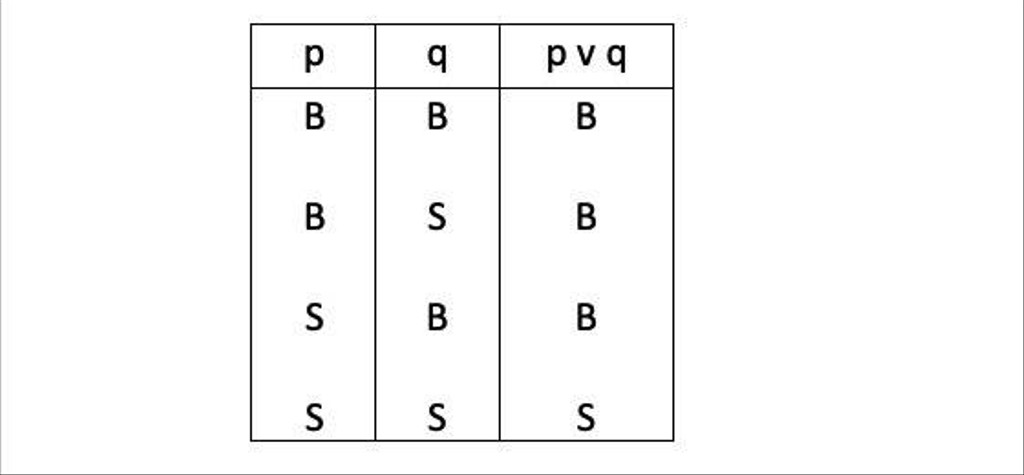
Disjungsi adalah pernyataan majemuk yang menggunakan kata hubung ‘atau’. Bentuk notasinya adalah “p ∨ q” yang kemudian dibaca “p atau q”. Sedulur dapat menyimak contohnya dalam gambar tabel di atas. Adapun keterangannya sebagai berikut:
- p = pernyataan 1
- q = pernyataan 2
- p ∨ q = p atau q
- B = benar
- S = salah
3. Implikasi (⇒)
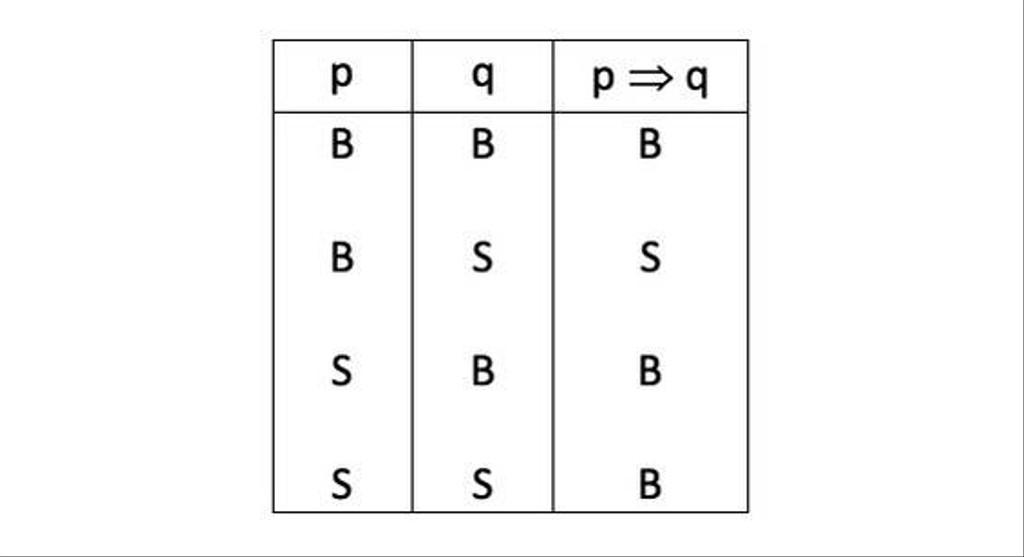
Sementara itu, implikasi adalah pernyataan majemuk yang menggunakan kata hubung ‘jika…maka…’. Sehingga bentuk notasi dari implikasi adalah “p ⇒ q” yang kemudian dibaca “Jika p, maka q”. Contohnya dapat Sedulur lihat dalam tabel yang ada dalam gambar di atas. Adapun keterangannya adalah sebagai berikut:
- p = pernyataan 1
- q = pernyataan 2
- p ⇒ q = jika p, maka q
- B = benar
- S = salah
4. Biimplikasi (⇔)
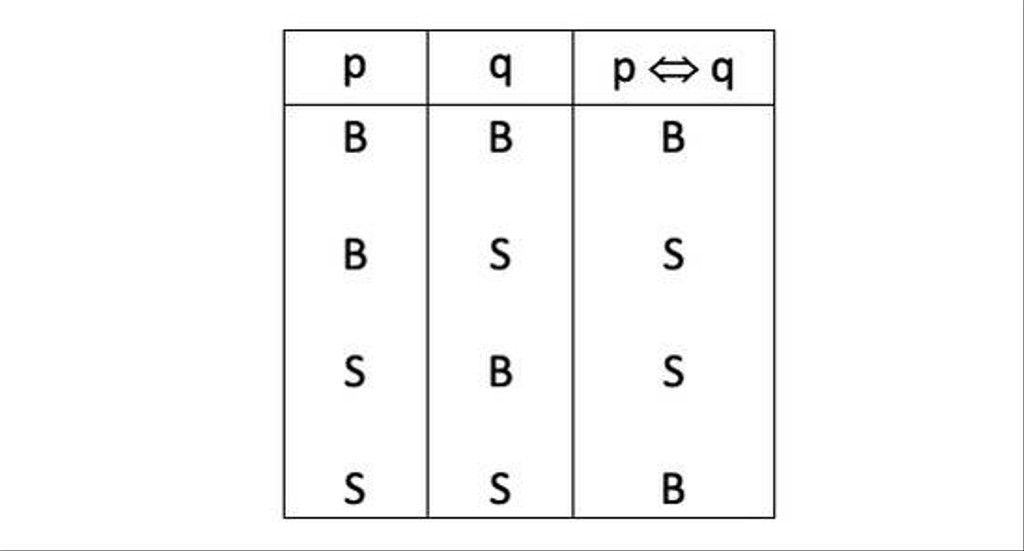
Biimplikasi adalah pernyataan majemuk yang menggunakan kata hubung ‘… jika dan hanya jika …”. Sehingga, bentuk notasinya adalah “p ⇔ q” yang kemudian dibaca “p jika dan hanya jika q”. Bentuk nilai kebenaran dari biimplikasi dapat dilihat dalam tabel di atas, dengan keterangan sebagai berikut:
- p = pernyataan 1
- q = pernyataan 2
- p ⇔ q = p jika dan hanya jika q
- B = benar
- S = salah
BACA JUGA: Rumus & Contoh Soal Perbandingan Senilai dan Berbalik Nilai
Fungsi tabel kebenaran

Secara singkat, telah dibahas di awal bahwa fungsi tabel kebenaran bertujuan untuk melihat nilai kebenaran pada sebuah premis dan pernyataan. Bukan hanya itu, tabel ini juga untuk melihat argumen yang valid dan tidak valid.
Dalam tabel kebenaran, diartikan sebagai tabel yang akan berisi kombinasi-kombinasi variabel masukan (input) yang akan menghasilkan keluaran (output) yang logis. Sebagaimana yang bisa Sedulur lihat dalam pembahasan yang telah dijelaskan di atas.
Tabel kebenaran juga berkaitan dengan logika dalam matematika. Logika sendiri terdiri dari beberapa gerbang logika atau logic gate. Dalam tabel kebenaran, terdapat beberapa jenis gerbang logika yang digunakan, yaitu sebagai berikut:
- Gerbang AND
- Gerbang OR
- Gerbang NOT
- Gerbang NAND
- Gerbang NOR
- Gerbang XOR
- Gerbang XNOR
Gerbang logika memiliki aturan dan cara kerjanya sendiri. Misalnya Gerbang AND yang memerlukan dua atau lebih input untuk menghasilkan satu output. Jika semua atau salah satu inputnya merupakan bilangan biner 0, maka outputnya akan menjadi 0. Sedangkan jika semua input adalah bilangan biner 1, maka outputnya akan menjadi 1.
Atau contoh lain misal gerbang XOR. Gerbang XOR ini memerlukan dua input untuk menghasilkan satu output. Jika input berbeda (misalkan: input A=1, input B=0) maka output yang dihasilkan adalah bilangan biner 1. Sedangkan jika input adalah sama maka akan menghasilkan output dengan bilangan biner 0.
Nah itulah penjelasan tentang tabel kebenaran, kini Sedulur mengetahui bagaimana cara membuatnya dan bagian-bagian penting didalamnya. Bukan hanya itu, Sedulur juga mengetahui fungsi dari tabel itu sendiri.



