Lingkaran merupakan salah satu bangun geometri atau bangun datar yang dipelajari dalam bidang ilmu matematika. Selain mempelajari rumus luas dan keliling lingkaran, ada pula materi mengenai persamaan lingkaran.
Secara sederhana, persamaan lingkaran adalah persamaan yang digunakan untuk menggambarkan lingkaran dalam diagram kartesius berdasarkan pusat dan jari-jarinya. Ada dua bentuk persamaan lingkaran yang perlu Sedulur pahami, yaitu bentuk standar dan bentuk umum.
Nah, untuk membantu Sedulur memahami materi persamaan lingkaran, berikut Super telah merangkum informasi selengkapnya. Mulai dari pengertian, macam-macam bentuk persamaan, hingga contoh soal dan pembahasannya. Yuk, langsung disimak!
BACA JUGA: Rumus Luas Lingkaran serta Cara Menghitung & Contoh Soalnya
Mengenal bangun datar lingkaran
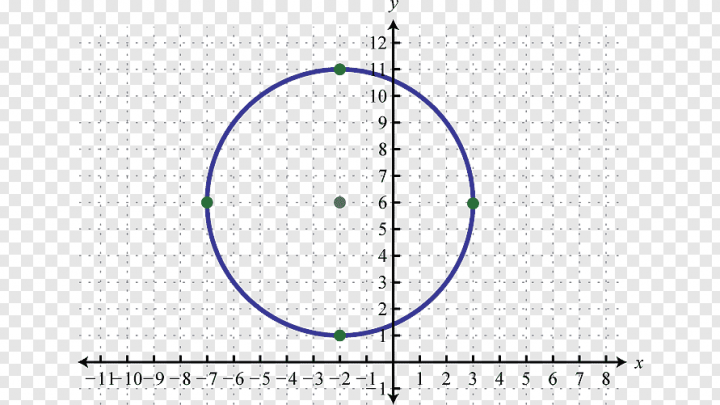
Sebelum masuk ke pembahasan yang lebih jauh, ada baiknya Sedulur memahami terlebih dahulu apa itu lingkaran.
Seperti yang sudah disinggung pada bagian pembuka, lingkaran merupakan sebuah bangun geometri atau bangun datar yang dibentuk dari kumpulan titik-titik dan memiliki jarak yang sama terhadap suatu titik pusat. Definisi lingkaran juga bisa dijelaskan sebagai garis melengkung yang kedua ujungnya bertemu pada jarak yang sama dari titik pusat.
Adapun titik yang dimaksud pada uraian pengertian di atas adalah titik pusat lingkaran. Sementara, jarak yang dimaksud adalah jari-jari lingkaran. Selain titik pusat dan jari-jari, lingkaran juga memiliki diameter, yaitu garis yang terbentang dari titik ujung ke titik ujung lainnya melalui titik pusat. Diameter juga kerap disebut sebagai dua kali jari-jari lingkaran.
BACA JUGA: Transformasi Geometri: Pengertian, Rumus dan Contoh Soalnya
Pengertian persamaan lingkaran
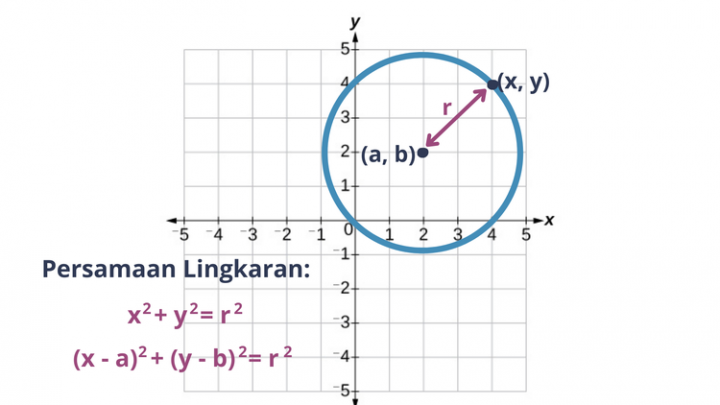
Sementara itu, persamaan lingkaran adalah cara aljabar yang digunakan untuk menggambarkan lingkaran pada diagram kartesius berdasarkan pusat dan panjang jari-jarinya. Persamaan ini menunjukkan koordinat dari titik pusat dan seluruh titik-titik yang membentuk keliling lingkaran.
Di sisi lain, persamaan lingkaran juga didefinisikan sebagai persamaan yang menyatakan hubungan variabel x dan variabel y yang membentuk lingkaran. Oleh sebab itu, rumus persamaan ini pun menggunakan kedua variabel tersebut yang ditentukan berdasarkan letak titik pusat dan panjang jari-jarinya.
Adapun secara umum dikenal dua bentuk rumus persamaan lingkaran, yaitu bentuk standar dan bentuk umum. Bentuk standar terbagi menjadi dua, yaitu persamaan dengan titik pusat (0, 0) dan titik pusat (a, b). Berikut penjelasan untuk masing-masing bentuk.
BACA JUGA: Persamaan Garis Lurus: Definisi, Rumus, Sifat & Contoh Soalnya
Persamaan lingkaran dengan titik pusat (0, 0) dan (a, b)

Bentuk standar persamaan lingkaran menggunakan titik pusat sebagai acuannya. Pada diagram kartesius, sebuah lingkaran bisa digambar dengan titik pusat (0, 0) sehingga berada tepat di perpotongan sumbu x dan sumbu y. Di sisi lain, sebuah lingkaran juga bisa memiliki titik pusat tidak tepat di titik (0, 0) sehingga berada di koordinat (a, b). Hal ini menyebabkan keduanya akan memiliki rumus persamaan yang berbeda pula.
- Persamaan lingkaran dengan titik pusat (0, 0)
Jika suatu lingkaran memiliki titik pusat (0, 0) dengan jari-jari r, maka dapat dituliskan rumus atau bentuk persamaannya sebagai berikut.
x² + y² = r²
Keterangan:
- x = koordinat satu titik keliling lingkaran terhadap sumbu x
- y = koordinat satu titik keliling lingkaran terhadap sumbu y
- r = jari-jari lingkaran
- Persamaan lingkaran dengan titik pusat di koordinat (a, b)
Sementara, jika titik pusat lingkaran tidak tepat (0, 0) atau berada pada koordinat (a, b), maka bisa dituliskan rumus persamaannya sebagai berikut.
- r² = (koordinat pusat di x – koordinat titik di x)² + (koordinat pusat di y – koordinat titik di y)²
- r² = (x – a)² + (y – b)²
- r = √(x – a)² + (y – b)²
Bentuk umum persamaan lingkaran
Persamaan bentuk standar juga bisa diubah ke bentuk umum yang merupakan hasil perluasan kuadrat binominal dalam bentuk standar dan penggabungan suku-suku sejenis. Bentuk umum ini diturunkan dari bentuk standar dan dapat dituliskan sebagai berikut.
- r² = (x – a)² + (y – b)² atau juga dapat ditulis (x – a)² + (y – b)² = r²
- (x – a)(x – a) + (y – b)(y – b) = r²
- x² – ax – ax + a² + y² – bx – bx + b² = r²
- x² + y² – 2ax – 2bx + a² + b² – r² = 0
Terdapat aturan di mana A = -2a, B = -2b, dan C = a² + b² – r². Sehingga diperoleh bentuk umum persamaan lingkaran sebagai berikut.
x² + y² + Ax + By + C = 0
Persamaan tersebut memiliki ketentuan, yaitu:
- titik pusat lingkaran = (-1/2 A, -1/2 B)
- jari-jari lingkaran = √1/4 A² + 1/4 B² – C
BACA JUGA: Rumus Persamaan Dasar Akuntansi Beserta Contohnya
Contoh soal dan pembahasan

Berikut beberapa contoh soal dan pembahasannya yang dapat Sedulur simak untuk lebih memahami materi ini.
Contoh 1
Sebuah lingkaran memiliki titik pusat (1, 2) dan jari-jari 5. Tentukan persamaan lingkaran tersebut!
Jawab:
Diketahui, titik pusat lingkaran = (1, 2) dan jari-jari lingkaran atau r = 5
Karena titik pusat lingkaran adalah (1, 2) atau (a, b), maka menggunakan rumus r² = (x – a)² + (y – b)² atau (x – a)² + (y – b)² = r² sehingga bisa dituliskan sebagai berikut.
- (x – a)² + (y – b)² = r²
- (x – 1)² + (y – 2)² = 5²
- (x – 1)(x – 1) + (y – 2)(y – 2) = 25
- x² – 2x + 1 + y² – 4y + 4 – 25 = 0
- x² + y² – 2x – 4y – 20 = 0
Maka, persamaan lingkaran dengan titik pusat (1, 2) dan jari-jari 5 adalah x² + y² – 2x – 4y – 20 = 0.
Contoh 2
Tentukan persamaan lingkaran yang memiliki titik pusat (3, 5) dan jari-jari 7!
Jawab:
Diketahui, titik pusat lingkaran = (3, 5) dan jari-jari lingkaran atau r = 7
Karena titik pusat lingkaran adalah (3, 5) atau (a, b), maka menggunakan rumus r² = (x – a)² + (y – b)² atau (x – a)² + (y – b)² = r² sehingga bisa dituliskan sebagai berikut.
- (x – a)² + (y – b)² = r²
- (x – 3)² + (y – 5)² = 7²
- (x – 3)(x – 3) + (y – 5)(y – 5) = 49
- x² – 6x + 9 + y² – 10y + 25 – 49 = 0
- x² + y² – 6x – 10y – 15 = 0
Maka, persamaan lingkaran dengan titik pusat (3, 5) dan jari-jari 7 adalah x² + y² – 6x – 10y – 15 = 0.
Demikian tadi pembahasan mengenai persamaan lingkaran, mulai dari pengertian, macam-macam bentuk atau rumus, dan contoh soal beserta pembahasannya. Semoga artikel ini dapat membantu Sedulur untuk memahami materi tersebut, ya!
Mau belanja bulanan nggak pakai ribet? Aplikasi Super solusinya! Mulai dari sembako hingga kebutuhan rumah tangga tersedia lengkap. Selain harganya murah, Sedulur juga bisa merasakan kemudahan belanja lewat handphone. Nggak perlu keluar rumah, belanjaan pun langsung diantar.
Bagi Sedulur yang punya toko kelontong atau warung, bisa juga lho belanja grosir atau kulakan lewat Aplikasi Super. Harga dijamin lebih murah dan bikin untung makin melimpah.



