Salah satu materi pelajaran Matematika yang dipelajari di bangku SMP adalah persamaan garis lurus. Persamaan yang sangat berguna dalam kehidupan sehari-hari ini dapat digunakan untuk menyelesaikan beberapa permasalahan, seperti misalnya pada kenaikan harga barang.
Sebenarnya, apa yang dimaksud persamaan garis lurus? Nah, secara mudahnya, merupakan persamaan yang membentuk garis lurus apabila digambarkan dalam bidang kartesius. Jika Sedulur tertarik mempelajari materi ini, simak informasi mengenai sifat, rumus, dan contoh soal berikut ini, ya!
BACA JUGA: Kumpulan Simbol Matematika Beserta Arti & Cara Membacanya
Definisi
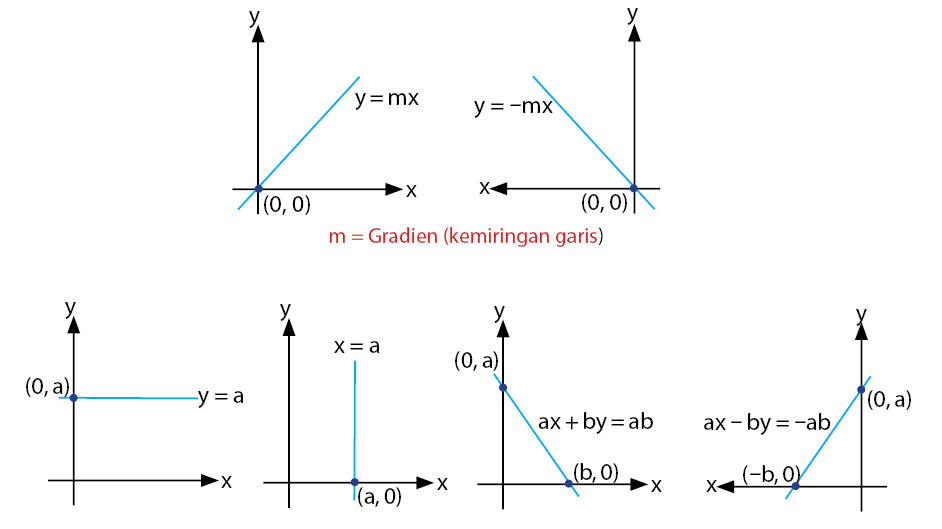
Garis lurus merupakan garis yang memiliki kemiringan stagnan atau sama pada setiap ruasnya. Pada suatu grafik, persamaan garis lurus akan memiliki perbandingan yang sama, atau dalam arti memiliki selisih koordinat y dan selisih koordinat x yang bernilai serupa.
Dalam mempelajari garis lurus, Sedulur tentu juga harus paham terlebih dahulu mengenai gradien. Hal ini karena konsep persamaan ini berkaitan dengan kemiringan garis atau gradien, yakni besarnya perbedaan tinggi (y) dibandingkan dengan besarnya perbedaan datar (x).
Gradien suatu garis dapat memiliki dua nilai, yakni bernilai positif dan negatif. Jika garisnya naik dari kiri ke kanan, maka gradiennya bernilai positif. Sebaliknya, jika garisnya turun dari kiri ke kanan, maka gradiennya bernilai negatif.
Nah, dari penjelasan di atas, dapat disimpulkan bahwa persamaan garis lurus adalah perbandingan selisih koordinat y dan selisih koordinat x yang membentuk garis lurus saat digambarkan dalam bidang Kartesius.
Sifat persamaan garis lurus
Ada beberapa sifat yang dimiliki oleh persamaan ini, yaitu:
- Garis lurus yang saling berimpit
- Garis lurus yang saling sejajar
- Garis lurus yang saling berpotongan
- Garis lurus yang saling tegak lurus
BACA JUGA: Rumus Persamaan Dasar Akuntansi Beserta Contohnya
Rumus persamaan garis lurus
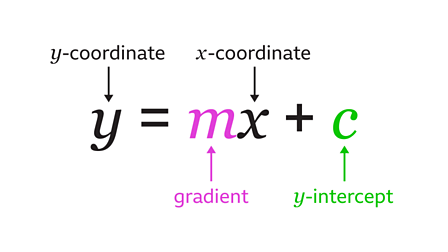
Dalam memahami materi ini, Sedulur juga harus mengetahui tentang rumus persamaan garis lurus. Rumus persamaan ini secara umum dinyatakan dalam dua bentuk, yakni bentuk eksplisit dan bentuk implisit.
Bentuk eksplisit adalah bentuk persamaan garis lurus dituliskan dengan y = mx + c dimana x dan y merupakan variabel sedangkan m dan c adalah konstanta. Dalam hal ini, m sering disebut koefisien arah atau gradien dari garis lurus.
Sehingga untuk garis yang persamaannya y = 2x + 1, nilai gradien m = 2.
Sementara itu, bentuk implisit merupakan bentuk persamaan yang dapat diubah menjadi bentuk yang lain. Misalnya pada persamaan y = 2x + 1, dapat diubah ke bentuk lain menjadi 2 x – y + 1 = 0.
Jadi, bentuk umum lain dari persamaan garis ini dapat dituliskan sebagai Ax + By + C = 0.
Selain dua bentuk tersebut, untuk mencari persamaan garis ini juga dapat dilakukan dengan dua cara. Pertama, menggunakan cara jika gradiennya diketahui dan garis melalui satu titik, dan kedua, menggunakan cara jika diketahui dua titik yang dilalui oleh garis.
Berikut adalah rumusnya:
- Diketahui gradien dan garis melalui satu titik, maka y – y1 = m (x– x1)
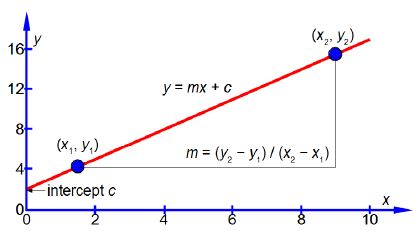
- Diketahui dua titik yang dilalui garis, maka: (y – y1)/(y2– y1) = (x– x1)/(x2– x1)
Cara menentukan dan menggambar persamaan garis lurus
Dalam menentukan persamaan garis lurus, Sedulur perlu mengetahui setidaknya dua hal penting. Pertama, Sedulur harus tahu nilai gradien dari garis tersebut, dan kedua, Sedulur harus tahu setidaknya satu titik yang dilalui garis tersebut.
Setelah mengetahuinya, Sedulur dapat menggambar persamaan garisnya dengan langkah-langkah berikut:
- Mencari titik potong pada sumbu x, y = 0.
- Mencari titik potong pada sumbu y, x = 0.
- Buat garis yang menghubungkan kedua titik potong.
BACA JUGA: Persamaan Kuadrat dalam Matematika Beserta Contoh Soalnya
Contoh soal
Berikut adalah beberapa contoh soal yang bisa Sedulur pelajari lebih lanjut.
- Buatlah grafik dari persamaan garis lurus y = 3x – 9!
Jawab:
Untuk mengerjakan soal ini, maka Sedulur perlu mengetahui hasil akhir yang diminta merupakan grafik dalam bidang kartesius. Jadi,
Pertama, cari titik potong pada sumbu x dengan membuat variabel y menjadi 0.
y = 3x – 9
0 = 3x – 9
3x = 9
x = 9/3
x = 3
Jadi, nilai x yang dihasilkan adalah 3, sehingga titik potong pada sumbu x adalah (3,0).
Kedua, cari titik potong di sumbu y dengan mengganti variabel x menjadi 0.
y = 3x – 9
y = 3(0) – 9
y = 0 – 9
y = -9
Jadi, nilai y yang dihasilkan adalah -9, sehingga titik potong sumbu y adalah (0, -9).
Setelah diketahui semua titik potongnya, Sedulur sudah bisa menggambar grafik persamaan garis tersebut dengan menghubungkan titik potong tersebut atau dengan menarik garis lurus yang menghubungkan kedua titik potong.
Berikut adalah hasilnya.
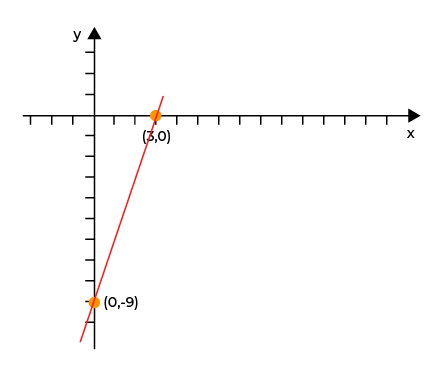
- Tentukan persamaan garis lurus jika diketahui informasi, sebagai berikut:
- Memiliki gradien = 3
- Melalui titik (2, 1)
Jawab:
Dalam mengerjakan soal ini, Sedulur dapat menggunakan dua rumus seperti yang telah disebutkan sebelumnya. Diketahui m = 3, x = 2, dan y = 1.
- Rumus pertama y – y1 = m(x– x1)
y – 1 = 3(x – 2)
y = 3x – 6 + 1
y= 3x – 5
- Rumus kedua y = mx + c
1 = 3(2) + c
1 = 6 + c
c = -5
y = 3x – 5
Jadi, persamaan garisnya adalah y = 3x – 5
- Persamaan garis lurus yang melewati titik (-1,1) dan (4,6) adalah?
Jawab:
Diketahui:
x1 = -1
x2 = 4
y1 = 1
y2 = 6
Ditanya:
Persamaan garisnya?
Dijawab:
(y – y1)/(y2– y1) = (x– x1)/(x2– x1)
(y – 1)/(6 – 1) = (x – (-1))/(4 – (-1))
(y – 1)/5 = (x + 1)/5
y – 1 = x + 1
y = x + 2
Nah, itulah informasi mengenai persamaan garis lurus yang meliputi definisi, rumus, sifat, hingga contoh soalnya. Semoga informasi ini dapat bermanfaat bagi Sedulur semuanya dalam mempelajari ilmu Matematika, ya!
Mau belanja bulanan nggak pakai ribet? Aplikasi Super solusinya! Mulai dari sembako hingga kebutuhan rumah tangga tersedia lengkap. Selain harganya murah, Sedulur juga bisa merasakan kemudahan belanja lewat handphone. Nggak perlu keluar rumah, belanjaan pun langsung diantar.
Bagi Sedulur yang punya toko kelontong atau warung, bisa juga lho belanja grosir atau kulakan lewat Aplikasi Super. Harga dijamin lebih murah dan bikin untung makin melimpah.



