Limit fungsi aljabar biasanya selalu dibahas ketika menginjakkan di bangku SMA, khususnya di kelas 11. Sudah sewajarnya Sedulur paham dengan pengertian hingga sifat-sifat di tingkatan tersebut. Secara sederhana, limit ini digunakan untuk menyatakan sesuatu yang nilainya mendekati nilai tertentu.
Materi limit fungsi aljabar sebaiknya memang tidak disederhanakan seperti itu. Untuk memahami seutuhnya, kita bisa bahas dari mulai pengertian, sifat-sifat, sampai contoh soal serta pembahasannya. Sedulur juga akan mengenal limit tak hingga yang merupakan angka besar yang nilainya tidak dapat dipastikan. Untuk itu, mari sama-sama bahas apa itu limit fungsi aljabar dan contohnya!
BACA JUGA: Rumus Volume Bola Serta Cara Menghitung & Contoh Soalnya
Pengertian limit fungsi aljabar
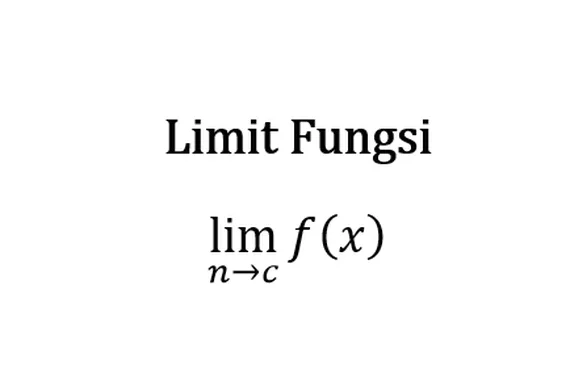
Limit adalah sebuah nilai yang menggunakan pendekatan fungsi ketika mendekati nilai tertentu. Limit bisa dikatakan sebagai nilai yang menuju suatu batas, sedangkan batasnya sendiri bisa dikatakan dekat tetapi sebenarnya tidak bisa dicapai.
Sebelum membahas lebih jauh, kamu juga harus ingat bahwa fungsi biasa ditulis f(x). Fungsi memiliki variabel yang jika kita substitusi suatu bilangan, maka ia akan menghasilkan nilai tertentu. Sebagai contoh, f(x) = 5x. Jika x=2, berarti f(x) = 5 X 2 = 10.
Sifat-sifat limit fungsi
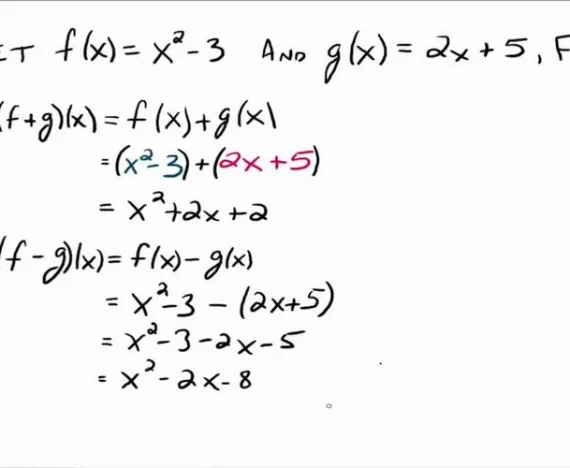
Sifat-sifat limit fungsi aljabar penting untuk diketahui karena akan berguna ketika Sedulur harus menentukan nilai suatu limit nantinya. Sifat-sifat ini ditentukan jika n adalah bilangan bulat positif, k konstanta, f dan g adalah fungsi-fungsi yang memiliki limit di c, maka selanjutnya berlaku teorema-teorema di bawah ini:
- lim x →a c = c
- lim x →a xn = an
- lim x →a c f(x) = c lim x →a f(x)
- lim x →a ( f(x) + g(x)) = lim x →a f(x) + lim x →a g(x)
- lim x →a ( f(x) x g(x)) = lim x →a f(x) x lim x →a g(x)
- lim x →a f(x)/g(x) = (lim x →a f(x))/(lim x →a g(x))
- lim x →a f(x)n = (lim x →a f(x))n
- lim x →a n√ f(x) = n√lim x →a f(x)
Sifat-sifat di atas wajib diingat karena akan sangat penting untuk memperdalam semua hal mengenai limit. Sifat-sifat limit fungsi aljabar dan contohnya akan lebih mudah dipahami jika dipelajari bersamaan. Adapun soal limit sangat beragam dan semakin lama bisa lebih kompleks.
Mencari nilai limit fungsi dengan pemfaktoran
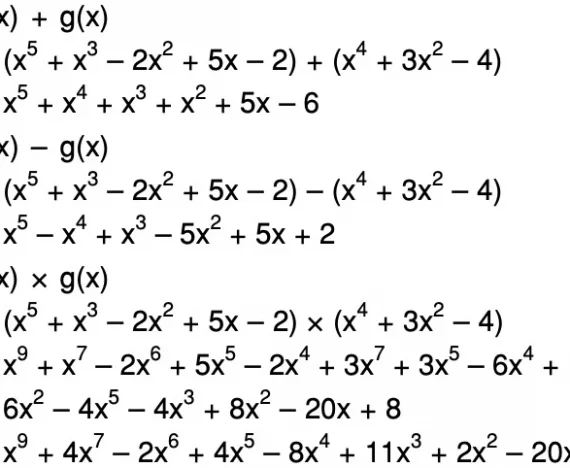
Untuk mengetahui nilai limit, terdapat 3 jenis metode yang bisa coba Sedulur lakukan. Metode tersebut adalah metode substitusi, pemfaktoran, dan mengalikan dengan faktor sekawan. Nah, berikut ini adalah metode-metodenya bersama dengan contoh soal limit fungsi serta pembahasannya.
1. Metode substitusi
Metode ini merupakan cara dasar yang sering digunakan oleh pemula yang baru mempelajari nilai limit. Caranya adalah dengan mensubstitusi langsung nilai ke dalam fungsi f(x). Contohnya:
- Lim x->2 1/2x + 5 = ½ X 2 + 5 = 1 + 5 = 6
2. Metode pemfaktoran
Limit fungsi aljabar pemfaktoran dilakukan ketika pada metode substitusi menghasilkan nilai tak tentu. Jika pada metode substitusi menghasilkan suatu nilai bentuk tak tentu seperti 0/0 dan bentuk tak tentu seperti tak hingga, maka fungsi tersebut harus difaktorkan terlebih dahulu, kemudian bisa disubstitusikan. Contoh soal:
- Lim x->2 x2 – 9/x – 3 = Lim x->2 (x – 3) (x + 3)/ x – 3 = Lim x->2 (x + 3) = 2 + 3 = 5
3. Metode mengalikan dengan faktor sekawan
Apabila pada metode substitusi akan menghasilkan nilai limit irasional, maka Sedulur bisa coba menggunakan limit fungsi aljabar bentuk akar. Fungsi dikalikan dengan akar sekawannya, lalu baru bisa disubstitusikan. Berikut ini contoh soalnya :
- Lim x->2 x – 7/ Vx – V7 = Lim x->2 x – 7/ Vx – V7 X x + 7/ Vx + V7 = Lim x->2 (x – 7) (Vx + V7)/ X-7 =
- Lim x->2 (Vx + V7) = V7 + V7 = 2V7
Limit tak hingga

Limit fungsi aljabar tak hingga adalah materi berikutnya yang harus Sedulur pahami. Fungsi limit tak hingga ini digunakan untuk menggambarkan keadaan limit x mendekati tak hingga atau dinotasikan dengan lim x → ∞ f(x).
Ada dua cara yang bisa Sedulur gunakan untuk menyelesaikan limit tak hingga ini dari suatu fungsi aljabar. Di bawah ini adalah cara serta contoh soal limit fungsi tak hingga. Di sana juga terdapat pembahasan untuk mempermudah Sedulur memahami keseluruhan proses pengerjaan pada limit tak hingga.
BACA JUGA: Rumus Keliling Segitiga Beserta Pembahasan & Contoh Soalnya
Soal dan pembahasan limit fungsi aljabar
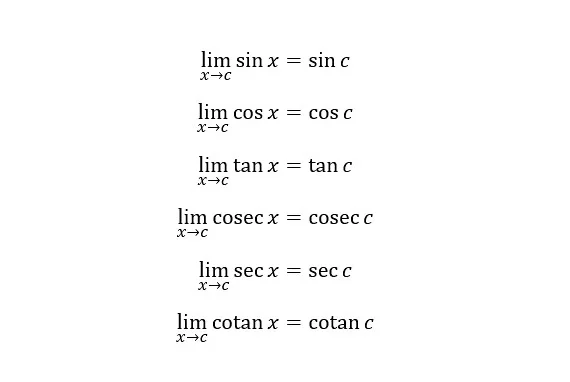
Berikut ini adalah contoh soal limit fungsi aljabar. Tujuannya agar Sedulur agar lebih mudah memahami penjelasan yang telah dibahas sebelumnya. Terdapat beberapa contoh yang bisa Sedulur pelajari, yaitu:
1. Bentuk tak tentu ∞/∞
- Lim x->∞ = anxn + an-1xn-1 + an-2xn-2 + an-3xn-3 + … / pmxm + pm-1xm-1 + am-2xm-2 + am-3xm-3 + … = L
- L = 0 jika dan hanya jika n < m
- L = a/p jika dan hanya jika n = m
- L = ∞ jika dan hanya jika n > m
Contoh Soal:
- Lim x->∞ = 4×3 – 3×2 + 2x – 1 / 5×3 +14xx – 7x + 2 = 4/5
- Lim x->∞ = x3 + 2x / x2 + 1 = ∞
2. Bentuk tak tentu ∞ – ∞
- Lim x->∞ = Vax2 + bx + c – Vpx2 + qx + r = L
- L = -∞ jika dan hanya jika a < p
- L = b-q / 2Va jika dan hanya jika a = p
- L = ∞ jika dan hanya jika a > p
Contoh Soal:
- Lim x->∞ = Vx2 + x + 1 – Vx2 + 2x = 1 – 2 / 2 V1 = – ½
- Lim x->∞ = V2x2 – x + 5 – V4x3 – 1 = – ∞
Demikian mengenai limit fungsi aljabar. Semoga materi, penjelasan, hingga contoh-contoh soal di atas bisa membantu Sedulur dalam memahami semua terkait limit fungsi. Meskipun Sedulur pernah belajar di bangku sekolah, namun penjelasan di atas bisa menyegarkan kembali ingatan Sedulur tentang limit fungsi aljabar.
Mau belanja bulanan nggak pakai ribet? Aplikasi Super solusinya! Mulai dari sembako hingga kebutuhan rumah tangga tersedia lengkap. Selain harganya murah, Sedulur juga bisa merasakan kemudahan belanja lewat handphone. Nggak perlu keluar rumah, belanjaan pun langsung diantar.
Bagi Sedulur yang punya toko kelontong atau warung, bisa juga lho belanja grosir atau kulakan lewat Aplikasi Super. Harga dijamin lebih murah dan bikin untung makin melimpah.



