Menghitung Akar Pangkat 2 Secara Cepat, Mudah & Tepat

Akar pangkat 2 merupakan salah satu perhitungan dalam matematika. Pada dasarnya menghitung penjumlahan akar tidak begitu sulit, terutama jika menghitung secara manual. Akar pangkat 2 bisa dihitung dalam tiga cara, perkalian, pembagian ataupun eliminasi. Ketiga cara tersebut bisa diterapkan dengan mudah.

Meskipun saat ini sudah terdapat kalkulator akar pangkat 2 yang bisa memudahkan Sedulur untuk menghitung akar dengan mudah, namun Sedulur tetap perlu mengetahui cara menghitung akan secara manual dan dengan mudah. Untuk itu, artikel kali ini hadir untuk menjelaskan bagaimana cara menghitung akar tersebut agar Sedulur bisa mudah mengetahuinya.

BACA JUGA: Cara Menghitung Pecahan Biasa dan Campuran yang Mudah

Pengertian akar pangkat 2

Akar pangkat 2 atau dikenal juga dengan nama akar kuadrat (suare root) merupakan kebalikan dari sebuah operasi pangkat 2 atau inversi pangkat 2 suatu bilangan. Nilai akar pangkat 2 suatu bilangan x adalah y dimana berlaku x = y², dengan x dan y bilangan real. Sehingga dapat ditulis √x = y dan dibaca “akar kuadrat dari x sama dengan y”.  Akar kuadrat dalam bahasa inggris disebut “square root“.

Konsep dasar perpangkatan dapat memudahkan Sedulur mengetahui perhitungan akar, sebagaimana Sedulur bisa simak dalam contoh di bawah ini, yang merupakan akar pangkat 2 dari 144:

• √144 = 12
• Karena 12² = 12 × 12 = 144

Berikut ini adalah contoh akar pangkat 2 dari 169, agar Sedulur lebih memahami konsep dasarnya:

• √169 = 13
• Karena 13² = 13 × 13 = 169

Selain contoh di atas, terdapat juga contoh akar pangkat 2 dari 225, untuk menyempurnakan pemahaman Sedulur terkait konsep dasar akar pangkat 2, yaitu:

• √225 = 15
• Karena 15² = 15 × 15 = 225

Fungsi akar 2

Fungsi akar 2 adalah adalah rasional jika dan hanya jika x adalah bilangan rasional yang dinyatakan dapat sebagai hasil bagi dari dua kuadrat sempurna. Di dalam istilah geometri, fungsi akar kuadrat memetakan luas dari persegi kepada panjang sisinya.

Tujuannya untuk memudahkan penghitungan agar bisa mendapatkan hasil yang dibutuhkan dengan cara super cepat. Sebagai contoh, akar pangkat 2 dari 2 adalah 4 karena 2 x 2 sama dengan 4. Dengan begitu menghitung tidak perlu sulit dengan cara yang super mudah.

Tabel akar pangkat 2

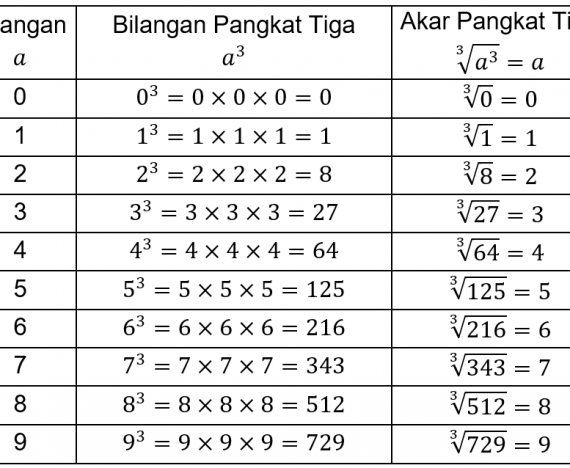
Agar lebih memudahkan Sedulur, berikut ini adalah tabel akar pangkat 2 yang bisa Sedulur jadikan referensi ketika menemui perhitungan akar. Tabel tersebut adalah sebagai berikut:

BACA JUGA: Rumus Luas Selimut Tabung dan Contoh Lengkap Soalnya

Akar Pangkat 3

Selain pangkat 2 terdapat juga pangkat 3. Pangkat 3 atau bilangan kubik dalam matematika (aritmetika dan aljabar) adalah hasil perkalian suatu bilangan n dua kali berturut-turut dengan dirinya sendiri, atau dikatakan mengalami pemangkatan tiga kali:

• n3 = n × n × n.

Juga merupakan hasil perkalian suatu bilangan dengan hasil kuadratnya:

• n3 = n × n2.

Ini juga merupakan rumus volume untuk kubus secara geometri di mana panjang sisinya adalah n, karena itu operasi ini disebut “kubik”. Fungsi invers operasi ini bertujuan menemukan bilangan yang hasil pangkat tiganya adalah n dengan cara mengekstraksi akar pangkat tiga bilangan n itu.

Ini digunakan untuk menghitung panjang sisi suatu kubus yang diketahui volumenya, yang juga merupakan pemangkatan ndengan bilangan sepertiga. Baik pangkat tiga dan akar pangkat tiga merupakan fungsi ganjil:

• (−n)3 = −(n3).

Pemangkatan tiga dari suatu bilangan atau ekspresi matematika lain dilambangkan dengan suatu superskrip 3, misalnya 23 = 8 atau (x + 1)3.

Fungsi kubik (pangkat 3)

Dalam matematika, sebuah fungsi kubik atau lebih dikenal sebagai fungsi pangkat tiga adalah suatu fungsi yang memiliki bentuk

• f(x)= ax3 + bx2 + cx + d

Dengan a bernilai tidak nol; atau dengan kata lain merupakan suatu polinomial orde tiga. Turunan dari suatu fungsi kubik adalah suatu fungsi kuadrat. Integral dari suatu fungsi kubik adalah fungsi pangkat empat (kuartik). Menetapkan ƒ(x) = 0 menghasilkan persamaan kubik. Biasanya, koefisien a, b, c, dan d merupakan bilangan riil. Untuk menyelesaikan persamaan kubik, caranya dengan mencari akar (nilai nol) dari fungsi kubik.

Rumus akar pangkat 2 dapat dihitung dengan tiga metode, yaitu perkalian, pembagian dan eliminasi. Berikut ini beberapa cara yang bisa Sedulur lakukan untuk menghitung akar pangkat 2:

BACA JUGA: 8 Cara Menghitung Luas Tanah untuk Rumah Mudah & Akurat

Contoh menghitung akar pangkat 2 dengan perkalian

Berikut ini adalah beberapa contoh menghitung akar pangkat dengan perkalian, yaitu:

• Akar kuadrat 4 adalah 2. Angka 4 merupakan bilangan bulat. Bilangan ini berasal dari perkalian 2×2 yang menghasilkan angka 4.
• Akar kuadrat 36 adalah 6. Angka 36 merupakan bilangan bulat. Bilangan ini berasal dari perkalian 6×6 yang menghasilkan angka 36.
• Akar kuadrat 64 adalah 8. Angka 64 merupakan bilangan bulat. Bilangan ini berasal dari perkalian 8×8 yang menghasilkan angka 64.

Contoh menghitung akar pangkat 2 dengan pembagian

Selain menggunakan perkalian, berikut cara menghitung akar pangkat dengan pembagian:

• Akar kuadrat 9 adalah 3. Angka yang bisa membagi 9 adalah angka 3, seperti 9:3 menghasilkan angka 3. Sudah tidak bisa dibagi lagi dan bisa dikalikan dengan dirinya sendiri.
• Akar kuadrat 25 adalah 5. Angka yang bisa membagi 25 adalah angka 5, seperti 25:5 menghasilkan angka 5. Sudah tidak bisa dibagi lagi dan bisa dikalikan dengan dirinya sendiri.

Contoh menghitung akar pangkat 2 dengan eleminasi

Berikut ini adalah contoh menghitung akar pangkat 2 dengan metode eleminasi. Mencari akar pangkat 2 bilangan tidak bulat 30. Akar pangkat 2 sempurna sebelum angka 30 adalah 25 yang menghasilkan angka 5. Itu artinya hasil hitungan kuadrat 30 mendekati angka 5 lebih sedikit.

Lakukan percobaan dengan 5.5 x 5.5 maka hasilnya 30.25 yang artinya terlalu banyak. Bisa dikurangi 0.1 dengan angka 5.4 seperti 5.4 x 5.4 maka hasilnya 29.14 yang artinya kurang dari 30. Selanjutnya kurangi 0.01 dengan angka 5.49 seperti 5.49 x 5.49 maka hasilnya 30.1401 yang artinya masih kelebihan. Lakukan pengurangan 0.022 dengan angka 5.478 seperti 5.478 x 5.478 maka hasilnya 30.008484.

Hasil 30.008484 menunjukkan hasil yang mendekati angka 30. Itu artinya hasil akar kuadrat 30 adalah 5.478. Untuk hasil lebih akurat lagi, bisa lakukan beberapa percobaan dan eliminasi.

Sekian penjelasan terkait akar pangkat 2, materi pelajaran matematika yang pernah kita dapatkan dari sejak bangku sekolah dasar hingga sekolah menengah atas. Namun, tentu saja tidak mudah mengingat rumus akar, dan artikel kali ini semoga dapat membantu Sedulur mengingat kembali perhitungan akar pangkat 2.

Sedulur yang membutuhkan sembako, bisa membeli di Aplikasi Super lho! Sedulur akan mendapatkan harga yang lebih murah dan kemudahan belanja hanya lewat ponsel. Yuk unduh aplikasinya di sini sekarang.