Salah satu konsep matematika yang dicetuskan oleh seorang matematikawan bernama Felix Klein adalah transformasi geometri. Konsep ini bermanfaat dalam melakukan banyak hal, seperti memindahkan setiap titik pada bidang menurut jarak dan arah tertentu.
Transformasi geometri dikenal sebagai sebuah perubahan pada suatu bidang geometri yang meliputi posisi, besar dan bentuknya sendiri. Tertarik belajar lebih dalam mengenai materi ini? Simak informasi selengkapnya berikut ini, yuk!
BACA JUGA: Rumus Integral Beserta Pengertian, Sifat & Contoh Soalnya
Pengertian transformasi geometri
Menurut KBBI, transformasi geometri diartikan berdasarkan dua kata penyusunnya, yakni transformasi dan geometri. Transformasi merupakan perubahan rupa (bentuk, sifat, fungsi, dan sebagainya) bisa juga perubahan struktur gramatikal lain dengan menambah, mengurangi, atau menata kembali unsur-unsurnya.
Sementara itu, geometri merupakan ilmu ukur dalam cabang matematika yang menjelaskan sifat-sifat garis, sudut, bidang hingga ruang. Dari dua pengertian tersebut, dapat disimpulkan bahwa transformasi geometri adalah perubahan rupa yang dapat dilihat dari garis, sudut, bidang, dan ruang.
Dalam konsep ini, jika hasil transformasi kongruen dengan bangunan yang ditransformasikan, maka disebut sebagai transformasi isometri. Transformasi isometri kemudian dibagi menjadi dua jenis lagi, yakni isometri langsung dan transformasi isometri berhadapan. Transformasi isometri langsung meliputi translasi dan rotasi, sedangkan transformasi isometri berhadapan meliputi refleksi.
Dalam pelajaran matematika, konsep ini dapat dinotasikan sebagai (x,y) sebagai posisi awal, dan (x’,y’) sebagai posisi akhir. Lebih jelasnya, selanjutnya akan dibahas jenis transformasi geometri beserta rumus-rumusnya.
Jenis transformasi geometri
Berikut adalah ulasan mengenai jenis-jenis transformasi geometri.
1. Translasi
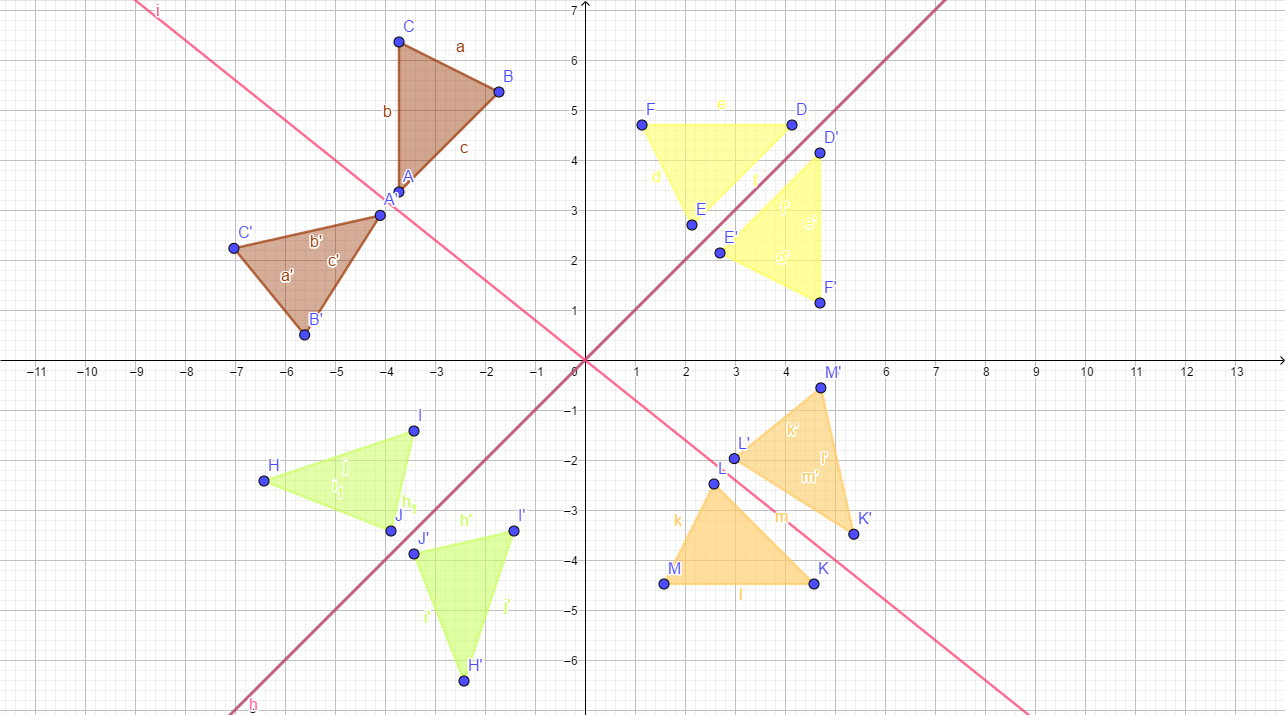
Translasi merupakan jenis transformasi yang memiliki jarak dan arah. Translasi ini dapat terjadi jika setiap titik pada bidang datar berpindah melalui jarak dan arah tertentu. Singkatnya, translasi hanya menggeser titik atau bidang sepanjang garis lurus dengan arah dan jarak, dan tidak mengubah ukuran sama sekali. Translasi umumnya disimbolkan dengan huruf T.
Pada translasi, yang berubah hanya posisinya saja. Sedangkan bentuk dan ukuran bidangnya masih tetap sama. Misalnya pada titik (x, y) yang ditranslasikan oleh ( a b ), maka hasilnya adalah bayangan ′ (x ′ , y ′ ) yang bisa ditulis dengan ( x′ y′ ) = ( x y ) + ( a b ).
Rumus translasi: (x′ y′ ) = ( x y ) + ( a b).
Keterangan:
(x, y) = titik asal
(x′ y′ ) = titik bayangan
(a b) = vektor translasi
2. Rotasi
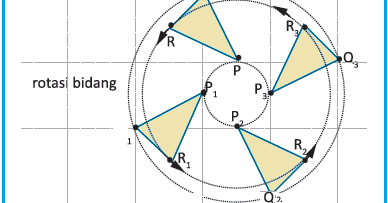
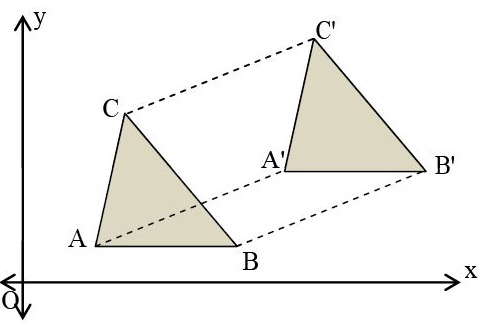
Sesuai dengan namanya, rotasi atau putaran merupakan bentuk transformasi yang dilakukan dengan memutar titik yang ada sebesar θ derajat. Perputaran pada bidang datar tersebut ditentukan oleh sebuah titik pusat rotasi, arah rotasi, dan besar sudut rotasi.
Dengan kata lain, rotasi merupakan transformasi geometri yang berupa pergeseran atau pemindahan semua titik pada bidang geometri sepanjang busur lingkaran yang memiliki titik pusat lingkaran sebagai titik rotasi. Rotasi dinotasikan dengan R (P,a) dimana P merupakan pusat rotasi dan a merupakan besar sudut rotasi.
Sudut rotasi berada di antara garis yang menghubungkan titik asal dengan pusat rotasi, sehingga menghubungkan titik bayangan dan pusat rotasi. Perlu diketahui bahwa arah putaran yang searah dengan jarum jam, dinyatakan sebagai arah negatif (-a), sedangkan arah putaran yang berlawanan dengan jarum jam, dinyatakan sebagai putar positif (a).
Ada beberapa rumus rotasi yang perlu dipahami, yaitu:
- Sudut putar 90°, maka x′ = – y dan y′ = x , maka (-y, x)
- Sudut putar – 90° atau 270°, jika pusat putar (0, 0), x′ = y dan y′ = – x, maka (y, -x)
- Sudut putar 180° dengan pusat putar (0, 0), x′ = – x dan y′ = – , maka (-x, -y)
- Sudut putar 90° dengan pusat putar (a, b): (x, y), maka (-y + a + b, x- a + b).
- Sudut putar 180° dengan pusat putar (a, b): (x, y), maka (-x +2a, -y +2b).
- Sudut putar – 90° dengan pusat putar (a, b): (x, y), maka (y – b +a, -x +a + b).
BACA JUGA: Hukum Coulomb adalah: Pengertian, Rumus & Contoh Soalnya
3. Refleksi
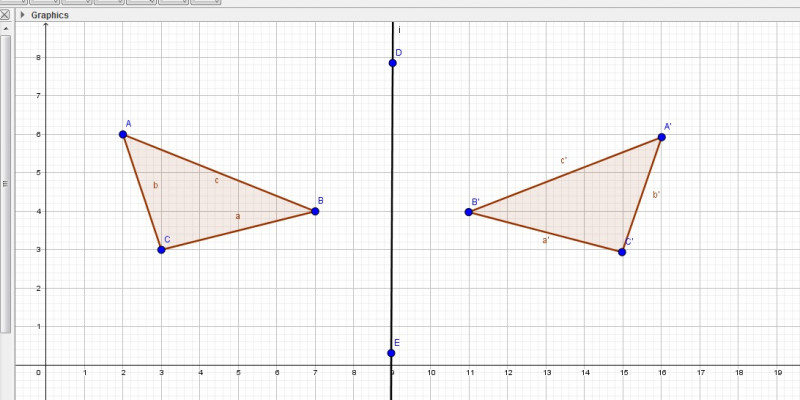
Refleksi merupakan jenis transformasi geometri yang bersifat seperti cermin. Jenis transformasi ini akan memindahkan titik bidang lewat sifat bayangan suatu cermin. Perubahan yang terjadi akan ditentukan dengan jarak dari titik asal ke cermin yang sama dengan jarak cermin ke titik bayangan.
Refleksi juga dapat didefinisikan sebagai pergeseran atau pemindahan semua titik pada bidang geometri menuju ke arah sebuah garis atau cermin dengan jarak yang sama dengan dua kali jarak titik ke cermin. Ada dua sifat penting dalam refleksi yang perlu dipahami, yaitu:
- Jarak titik ke cermin sama dengan jarak bayangan titik ke cermin.
- Geometri yang direfleksikan berhadapan dengan petanya.
Pencerminan yang terjadi bersifat isometris, yakni berukuran tetap atau sama. Bangun hasil atau bayangan akan kongruen dengan bangun asalnya. Garisnya juga akan menghubungkan titik asal dengan titik bayangan yang tegak lurus terhadap cermin. Dengan demikian, garis-garis yang terbentuk akan saling sejajar.
Rumus refleksi:
- Refleksi sumbu – x: (x, y), maka (x, -y)
- Refleksi sumbu – y: (x, y), maka (-x, y)
- Refleksi garis y = x: (x, y), maka (y, x)
- Refleksi garis y = x: (x, y), maka (-y, -x)
- Refleksi garis x = h: (x, y), maka (2h -x, y)
- Refleksi garis y = k: (x, y), maka (x, 2k – y)
4. Dilatasi
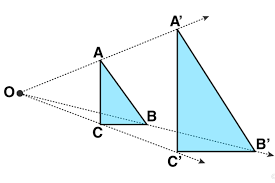
Dilatasi merupakan transformasi yang terjadi pada ukuran suatu objek. Dilatasi juga disebut sebagai transformasi similaritas (kesebangunan), yakni perubahan dengan mengubah jarak titik-titik dengan faktor pengali tertentu terhadap suatu titik tertentu yang tidak mengubah arahnya namun mengubah ukurannya.
Singkatnya, dilatasi merupakan transformasi berupa perkalian yang memperbesar atau memperkecil suatu bangunan geometri. Dalam konsep dilatasi, ada dua hal yang penting untuk diperhatikan, yakni titik dilatasi dan faktor dilatasi.
Titik dilatasi merupakan titik yang menentukan posisi suatu dilatasi. Titik ini menjadi titik pertemuan dari semua garis lurus yang menghubungkan titik-titik dalam suatu bangun ke titik-titik hasil dilatasi.
Sementara itu, faktor dilatasi merupakan faktor perkalian suatu bangun geometri yang didilatasikan. Faktor ini dapat menunjukan seberapa besar hasil dilatasi terhadap bangun geometri yang dinotasikan dengan k.
Nilai k > 1 atau k < -1 menunjukan hasil dilatasi yang lebih besar dari geometrinya. Sementara nilai -1 < k < 1 menunjukan hasil dilatasi lebih kecil dari geometrinya. Tanda positif juga dapat diartikan jika geometri dan hasil dilatasi berdampingan di salah satu sisi titik dilatasi, sedangkan tanda negatif dapat diartikan bahwa geometri dan hasil dilatasi saling terbalik dan berlainan sisi di titik dilatasi.
Pusat dilatasi merupakan faktor skala atau titik tertentu dilatasi. Dalam ilmu matematika, dilatasi dinotasikan dengan D (P, k) yang mana P adalah pusat dilatasi dan k adalah faktor skala. Semua garis yang melalui pusat dilatasi invarian terhadap sembarang dilatasi adalah (k≠0). Jika, |k | > 1, maka bangun hasil diperbesar dari ukuran semula, sedangkan jika | k | < 1, maka bangun hasil akan diperkecil dari ukuran semula.
Berdasarkan koordinat titik asal A (x, y), yang didilatasikan dengan faktor skala k terhadap pusat (0, 0), dan pusat (a, b). Maka, rumus dilatasi adalah sebagai berikut.
- Dilatasi titik pusat (0,0), dan faktor skala k: (x, y), maka (kx, ky).
- Dilatasi titik pusat (0,0) dan faktor skala k: (x, y), maka kx = k (x – a) + a, k (y – b) + b.
BACA JUGA: Rumus Usaha dalam Fisika Beserta Contoh Soal & Pembahasan
Contoh dalam kehidupan sehari-hari

Transformasi geometri dapat kita temukan dengan mudah dalam kehidupan sehari-hari. Beberapa contohnya adalah perubahan posisi ketika berjalan, berlari, melompat, dan pergerakan apapun yang mengakibatkan adanya perubahan posisi.
Selain itu, contoh penerapan transformasi geometri juga dapat ditunjukkan pada saat bercermin. Jarak benda dengan cermin akan sama dengan jarak cermin dengan bayangan. Tak hanya itu, saat melakukan gerakan berputar, itu juga merupakan contoh transformasi rotasi.
Contoh soal

- Tentukan bayangan titik A dengan A(-1,4) jika direfleksikan terhadap garis y = -x!
Jawab:
Apabila titik A(x,y) direfleksikan terhadap garis y = -x, maka bayangan titik A adalah A’ (-y,-x).
Jadi, bayangan titik A(-1,4) adalah A’(-4,1).
- Tentukan bayangan titik P(5,4) jika didilatasikan terhadap pusat (-2,-3) dengan faktor skala -4!
Jawab:
Diketahui P(x,y) = P(5,4). Pusat dilatasi di (a,b) = (-2,-3) dan k = -4.
Misalkan bayangan titik P berada di koordinat (x’,y’), maka
x’ = k(x-a) + a
x’ = -4(5-(-2)) + (-2)
x’ = -4(7) – 2
x’ = -30
y’ = k(y-b) + b
y’ = -4(4-(-3)) + (-3)
y’ = -4(7) – 3
y’ = -31
Jadi, koordinat bayangan titik P adalah (-30, -31)
Nah, itulah informasi mengenai transformasi geometri yang meliputi pengertian, jenis, rumus, contoh dalam kehidupan sehari-hari, dan contoh soalnya. Semoga informasi ini dapat bermanfaat bagi Sedulur semuanya dalam mempelajari ilmu Matematika, ya!
Mau belanja bulanan nggak pakai ribet? Aplikasi Super solusinya! Mulai dari sembako hingga kebutuhan rumah tangga tersedia lengkap. Selain harganya murah, Sedulur juga bisa merasakan kemudahan belanja lewat handphone. Nggak perlu keluar rumah, belanjaan pun langsung diantar.
Bagi Sedulur yang punya toko kelontong atau warung, bisa juga lho belanja grosir atau kulakan lewat Aplikasi Super. Harga dijamin lebih murah dan bikin untung makin melimpah.



