Rumus simpangan rata rata merupakan rumus yang ditemui dalam ilmu statistika. Dalam perhitungan ukuran penyebaran data, termasuk untuk analisis data deskriptif, rumus ini sangat dibutuhkan. Ukuran penyebaran data bertujuan untuk melihat seberapa besar penyimpangan data-data statistik. Dalam sistem perhitungan global, biasanya rumus ini dikenal dengan nama deviasi mean.
Ukuran penyebaran dibutuhkan untuk menguji reabilitas rata-rata pada kumpulan statistik. Rumus simpangan rata rata, merupakan salah satu dari enak cama menentukan ukuran penyebaran data statistik. Agar lebih memahaminya, yuk mari kita simak terlebih dahulu pengertian dari simpangan rata-rata terlebih dahulu.
BACA JUGA: Energi Potensial adalah: Pengertian, Jenis dan Rumusnya
Pengertian simpangan rata-rata
Nilai simpangan rata-rata adalah jumlah semua nilai mutlak simpangan dibagi dengan banyaknya data. Simpangan rata-rata dibagi menjadi dua yaitu rata-rata data tunggal dan data berkelompok. Simpangan rata-rata atau juga dikenal dengan deviasi mean merupakan nilai rata-rata dari selisih setiap data dengan nilai mean atau rataan hitungnya.
Deviasi mean sering dilambangkan dengan SR. Ragam atau variasi adalah nilai yang menunjukkan besarnya penyebaran data pada kelompok data.
Rumus simpangan rata rata
Berikut ini adalah rumus dari deviasi mean, yaitu:
SR=n1i=1∑n∣xi−xˉ∣,
Keterangannya yaitu Sekumpulan data kuantitatif yang tidak dikelompokkan serta dinyatakan oleh x1, x2, …, xn. Dari data tersebut dapat ditentukanlah simpangan rata-rata atau deviasi mean (SR).
Rumus simpangan dari data tunggal
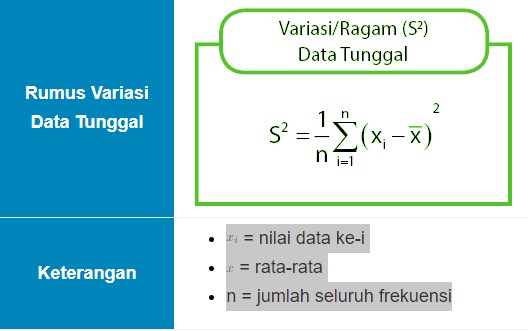
Selain rumus di atas, terdapat juga rumsu dari data tungguk atau variasi lainnya. Rumusnya sebagaimana yang dapat dilihat dalam gambar di atas. Adapun keterangan dari rumus di atas yaitu:
- x{i} = nilai data ke-i
- {x} = rata-rata
- n = jumlah seluruh frekuensi
Rumus simpangan dari data berkelompok
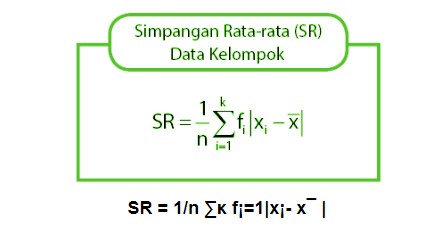
Selain dua rumus di atas, terdapat juga rumus simpangan dari data berkelompok. Rumusnya bisa Sedulur lihat pada gambar di atas, dengan keterangan sebagai berikut ini:
- n = jumlah seluruh frekuensi
- f{i} = frekuensi kelas ke-i
- x{i} = nilai tengah kelas ke-i
- {x} = rata-rata
- k = banyaknya kelas interval
BACA JUGA: Cara Menghitung Skala Peta Beserta Rumus & Contoh Soalnya
Contoh soal 1
Untuk memudahkan Sedulur memahami rumus ini, berikut contoh soal pertama yang bisa Sedulur pahami. Diberikan data sebagai berikut:
- 5, 6, 8, 5, 7
- Tentukan nilai SR data di atas!
Pembahasan:
Langkah awal terlebih dulu temukan rata-rata datanya: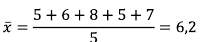
Setelah diketahui rata-ratanya, saatnya mencari SR:
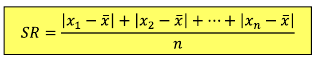.Sehingga nilainya, yaitu:
- SR = | 5-6,2|+|6-6,2|+8 -6,2|+ |5 -6,2|+|7 -6,2| / 5
- SR = 1,2 +0,2 +1,8 +1,2 +0,8/5 = 5,2/5 =1,04
Contoh soal 2
Perhatikan tabel distribusi frekuensi data dibawah ini
| Nilai | Frekuensi |
| 11 – 15 16 – 20 21 – 25 26 – 30 31 – 35 |
2 2 10 9 4 |
Tentukan nilai SR data di atas
Pembahasan:
Temukan terlebih dulu titik tengah setiap kelas, untuk kemudian dicari reratanya:
| Nilai | Frekuensi | x |
| 11 – 15 16 – 20 21 – 25 26 – 30 31 – 35 |
2 2 10 9 4 |
13 18 23 28 33 |
Rata-ratanya adalah:
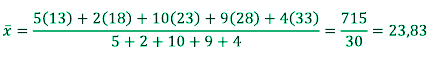
Contoh soal 3
Hitunglah SR dari data kuantitatif berikut :12, 3, 11, 3, 4, 7, 5, 11
Pembahasan:
Maka, nilai deviasi mean adalah 3,25.
Pada suatu sekumpulan data bisa dinyatakan oleh x1, x2, …, xn kemudian masing-masing nilai data tersebut mempunyai frekuensi f1 , f2 , …, fn maka diperolehlah nilai deviasi mean (SR) dengan menggunakan rumus di atas.
Nah itulah penjelasan terkait rumus simpangan rata rata yang bisa Sedulur pahami. Semoga penjelasan di atas membantu Sedulur untuk memahami rumus dan perhitungan statistik satu ini.
Mau belanja bulanan nggak pakai ribet? Aplikasi Super solusinya! Mulai dari sembako hingga kebutuhan rumah tangga tersedia lengkap. Selain harganya murah, Sedulur juga bisa merasakan kemudahan belanja lewat handphone. Nggak perlu keluar rumah, belanjaan pun langsung diantar.
Bagi Sedulur yang punya toko kelontong atau warung, bisa juga lho belanja grosir atau kulakan lewat Aplikasi Super. Harga dijamin lebih murah dan bikin untung makin melimpah.
