Keliling lingkaran sudah diajarkan sejak sekolah dasar. Lingkaran merupakan garis melengkung yang kedua ujungnya bertemu pada jarak sama dari titik pusat. Kedudukan titik-titik pada bidang datar berjarak sama dengan sebuah titik tertentu pada bidang tersebut. Titik tertentu itu disebut sebagai titik pusat lingkaran.
Berikut ini akan dibahas tentang pengertian bangun datar lingkaran, termasuk rumus keliling lingkaran diameter, contoh soal serta cara penyelesaiannya. Yuk, simak pembahasannya supaya lebih paham, Sedulur!
BACA JUGA: Konduksi: Pengertian, Ciri-Ciri, Perbedaan dan Contohnya
1. Pengertian lingkaran

Lingkaran adalah bangun datar yang semua titik pada lingkaran mempunyai jarak sama dari titik pusatnya. Jarak antara titik mana pun pada lingkaran dengan titik pusat disebut dengan jari-jari. Beberapa bagian dari lingkaran adalah sebagai berikut.
- Titik pusat (O) adalah titik tengah dari lingkaran di mana jarak titik tersebut dengan titik mana pun pada lingkaran selalu tetap.
- Jari-jari (r) adalah garis lurus yang menghubungkan titik pusat dengan titik pada lingkaran. Bagian ini merupakan jarak antara titik pusat dengan titik pada lingkaran.
- Tali busur yaitu garis lurus dalam lingkaran yang memotong lingkaran pada dua titik yang berbeda.
- Busur adalah garis lengkung pada lingkaran.
- Keliling lingkaran adalah busur terpanjang pada lingkaran.
- Diameter (2r) yaitu tali busur terpanjang yang melalui titik pusat disebut diameter. Panjang diameter merupakan dua kali dari jari-jarinya di mana diameter ini membagi lingkaran dua bagian yang sama luasnya.
- Apotema adalah garis terpendek antara tali busur dan pusat lingkaran.
- Juring yaitu daerah pada lingkaran yang dibatasi oleh busur dan dua buah jari-jari.
- Tembereng merupakan daerah di lingkaran yang dibatasi oleh sebuah busur dengan tali busurnya.
2. Rumus keliling lingkaran

Keliling lingkaran adalah busur terpanjang pada suatu lingkaran. Cara menghitung rumus lingkaran cukup mudah. Rumusnya dapat dihitung dengan mengetahui Pi (π) dan jari-jari atau radius lingkaran (r) atau diameter lingkaran (d). Rumusnya adalah K = 2πr atau K = πd. K merupakan lambang keliling. Sedangkan nilai π yaitu 22/7 atau 3,14.
- Jika diketahui diameter, maka rumus kelilingnya yaitu K = πd
- Jika diketahui jari-jari, maka rumus kelilingnya adalah K = 2πr
Contoh soal
Berapa keliling lingkaran yang mempunyai jari-jari 14 cm?
a. 54 cm
b. 66 cm
c. 88 cm
d. 110 cm
Pembahasan:
Jari-jari = r = 14 cm
Rumus = 2πr
K = 2 x (22/7) x 14 cm
K = 88 cm
Maka jawaban yang benar adalah C.
Contoh soal kedua
Jika garis tengah sebuah lingkaran sepanjang 20 cm, berapa keliling lingkaran tersebut?
a. 78 cm
b. 62,8 cm
c. 110 cm
d. 88,5 cm
Pembahasan:
Garis tengah = diameter = d = 20 cm
Rumus = πd
K = 3,14 x 20 cm
K = 62,8 x cm
Maka, jawaban yang benar adalah 62,8 cm
Contoh soal ketiga
Sebuah lingkaran mempunyai diameter 28 cm. Hitunglah keliling lingkaran tersebut!
Pembahasan:
K = πd
K = 22/7 × 28 K = 88 cm
Maka, hasilnya adalah 88 cm
BACA JUGA: Pengertian Frasa Beserta Jenis-Jenisnya & Contohnya
3. Setengah lingkaran
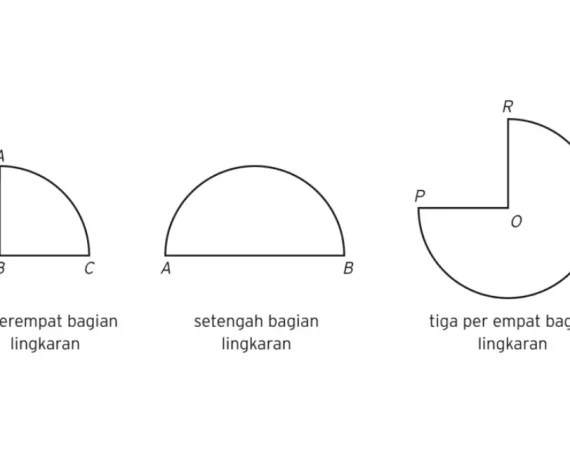
Setengah lingkaran merupakan bagian lingkaran yang diperoleh dari sebuah lingkaran penuh yang terbagi menjadi dua sama besar. Dapat diartikan bahwa setengah lingkaran merupakan lingkaran dalam bentuk setengah. Jika sebuah lingkaran dibagi empat sama besar, maka dinamakan seperempat lingkaran.
4. Rumus mencari luas setengah lingkaran
Rumus luas = π r2 / 2
Rumus mencari keliling setengah lingkaran:
Keliling = π D / 2, atau
Keliling = π r
5. Rumus keliling setengah lingkaran

Keliling lingkaran penuh dapat dihitung dengan rumus sebagai berikut:
K = 2 x π x r
Sedangkan rumus keliling setengah lingkaran dapat dihitung dengan rumus:
Keliling setengah lingkaran = π x r
Contoh soal keliling setengah lingkaran
Hitunglah keliling setengah lingkaran dengan jari-jari 14 cm.
Pembahasan:
K = (π x r) + d
K = (22/7 x 14) + (14 x 2)
K = (22/7 x 14) + (14 x 2)
K = 44 + 28
K = 72 cm
Jadi, keliling setengah lingkaran adalah 72 cm.
Sedulur pasti menemui banyak sekali benda yang berbentuk lingkaran. Lingkaran merupakan tempat kedudukan titik-titik yang berjarak sama dengan satu titik tertentu. Yang dimaksud titik tertentu di sini adalah titik pusat lingkaran, sedangkan jarak yang sama adalah jari-jari lingkaran. Sementara unsur-unsur lingkaran terdiri dari tirik pusat (p), jari-jari (r), diameter (d), busur lingkaran, tali busur, juring lingkaran, tembereng, dan apotema.
Demikianlah penjelasan mengenai rumus luas dan keliling lingkaran serta contoh soalnya. Semoga dengan artikel ini Sedulur lebih memahami tentang rumus lingkaran. Selamat belajar!



