Deret Fibonacci adalah rangkaian deret angka yang disusun berdasarkan penjumlahan dari dua angka sebelumnya. Penggunaan materi matematika ini biasanya banyak dijumpai dalam soal-soal untuk pendaftaran kerja maupun tes kelulusan.
Selain itu, Fibonacci sendiri dapat diterapkan untuk berbagai bidang, seperti bidang ekonomi dan juga sistem trading. Agar lebih memahami tentang apa itu Fibonacci, berikut penjelasan tentang deret Fibonacci lengkap beserta contoh dan juga manfaatnya. Yuk simak dengan seksama ya!
BACA JUGA : Pengertian Pendapatan Nasional Beserta Rumus & Manfaatnya
Definisi Fibonacci

Fibonacci merupakan suatu barisan bilangan hasil dari penjumlahan dua bilangan sebelumnya. Bilangan ini dikembangkan oleh Leonardo da Pisa atau yang juga dikenal dengan Fibonacci pada abad ke-13. Sebelumnya deret Fibonacci ditemukan oleh Gopala Chandra yang merupakan seorang ahli matematika dari India.
Bilangan Fibonacci
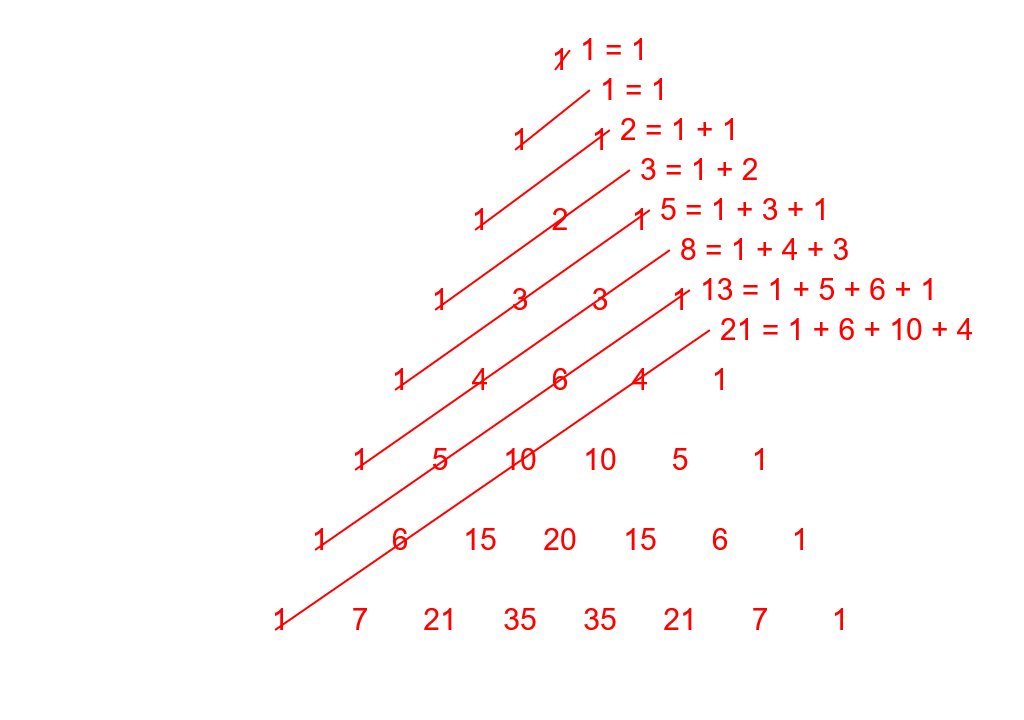
Dua bilangan Fibonacci pertama pertama adalah bilangan 0 dan 1. Sehingga suku-suku berikutnya dari barisan tersebut yaitu sebagai berikut.
Bilangan pertama: 0
Bilangan kedua: 1
Bilangan ketiga: 0 + 1 = 1
Bilangan keempat: 1 + 1 = 2
Bilangan kelima: 1 + 2 = 3
Bilangan keenam: 2 + 3 = 5
Bilangan ketujuh: 3 + 5 = 8
Bilangan kedelapan: 5 + 8 = 13
Dan seterusnya sehingga bilangan selanjutnya merupakan hasil dari penjumlahan dari dua bilangan sebelumnya. Tak hanya itu, konsep Fibonacci juga digunakan untuk barisan bilangan yang lainnya. Untuk lebih jelasnya, perhatikan contoh di berikut ini.
4, 5, 9, 14, 23, . . .
Pada barisan di atas, suku pertama: 4 dan suku kedua: 5.
Suku ketiga: 4 + 5 = 9,
Suku keempat: 5 + 9 = 14,
Suku kelima: 9 + 14 = 23,
dan seterusnya.
BACA JUGA : Rumus Keliling Lingkaran Beserta Contoh Soal & Pembahasan
Deret fibonacci adalah
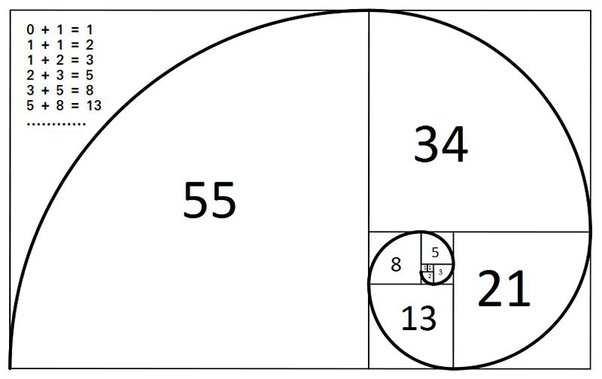
Deret Fibonacci diartikan secara rekursif atau berulang. Contohnya jika dalam beberapa pola barisan bilangan dengan dua suku pertama F1 = 0 dan F2 = 1.
Suku selanjutnya dirumuskan secara rekursif sebagai berikut.
Fn + 1 = Fn – 1 + Fn
Fibonacci Sequence (Deret angka Fibonacci)

Istilah ini adalah deret angka yang diperoleh dengan menjumlahkan dua angka sebelumnya. Maka Sedulur bisa menjumpai cara menemukannya seperti berikut ini.
1, 1, 2, …
1 + 2 = 3 maka 1, 1, 2, 3, …
2 + 3 = 5 maka 1, 1, 2, 3, 5, …
3 + 5 = 8 maka 1, 1, 2, 3, 5, 8, …
Dan begitupun seterusnya. Salah satu hal penting dalam Fibonanci adalah dengan mengenal Golden Ratio / Golden Mean / Phi (φ).
Golden Ratio / Golden Mean / Phi (φ)

Golden Ratio atau Golden Mean Fibbonanci merupakan hasil pembagian dari dua angka yang berurutan dalam deret angka Fibonacci. Golden ratio pada dasarnya terdiri dari 2 angka, yaitu: 1.618 dan 0.618. Angka ini disebut sebagai Golden Ratio juga bukan tanpa alasan karena:
- Hasil pembagian suatu angka Fibonacci terhadap angka Fibonacci sebelumnya selalu menghasilkan angka mendekati 1.618.
- Hasil pembagian suatu angka Fibonacci terhadap angka Fibonacci sesudahnya selalu menghasilkan angka mendekati 0.618.
Umumnya deret Fibonanci terdiri dari beberapa angka seperti: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, …
BACA JUGA : Brainstorming: Pengertian, Metode & Cara Melakukannya
Deret Fibonacci rumus
Rumus deret Fibonacci dapat diihitung dengan cara berikut ini.
fn = 1/√5 x ((1 + √5)/2)n – 1/√5 x ((1 – √5)/2)n
Contoh Fibonacci

Berikut contoh soal yang dapat Sedulur pelajari.
- Terdapat barisan bilangan sebagai berikut: 1, 1, 2, 3, 5, 8, . . .
Pertanyaan:
Tentukan suku ke-8 barisan tersebut!
Pembahasan
Dengan menerapkan konsep bilangan Fibonacci, maka diperoleh:
Suku ke-5 = 5
Suku ke-6 = 8
Suku ke-7 = 5 + 8 = 13
Suku ke-8 = 8 + 13 = 21
-
Perhatikan barisan bilangan berikut: 4, 7, 11, 18, 29, . . .
Pertanyaan:
Tentukan tiga suku selanjutnya dari barisan di atas!
Pembahasan
Suku ke-4 = 18
Suku ke-5 = 29
Suku ke-6 = 18 + 29 = 47
Suku ke-7 = 29 + 47 = 76
Suku ke-8 = 47 + 76 = 123
Tiga suku berikutnya yaitu 47, 76, dan 123.
BACA JUGA : Arti Konsumtif Beserta Faktor, Tanda & Cara Menghindarinya
Manfaat deret Fibonacci

Perlu Sedulur ketahui bahwa deret Fibonacci erat kaitannya dengan rasio emas, bilangan phi dan juga bilangan irrasional. Fibonacci juga dapat diterapkan pada berbagai pasar dalam mengidentifikasi kemungkinan level support atau resistance.
Contohnya seperti Fibonacci Retracements digunakan oleh trader di pasar foreign exchange (Forex). Namun belakangan, analisis ini juga sering digunakan dalam analisis teknikal cryptocurrency.
Fibonacci untuk trading
Terdapat beberapa tipe garis Fibonacci yang biasanya digunakan untuk trading. Diantara yaitu sebagai berikut.
- Fibonacci Retracement – Price only.
- Fibonacci Extension / Expansion / Projection – Price only.
- Fibonacci Fan – Price only.
- Fibonacci Arcs – Price and Time.
- Fibonacci Timezones – Time only.
Fakta menarik deret Fibonacci

1. Kesesuaian dengan komposiis tubuh manusia
Dari penelitian yang telah dilakukan, golden ratio (1,618) ditemukan dalam banyak bukti penyusunan tubuh manusia. Diyakini juga bahwa jika seseorang mengukur wajahnya kemudian dibagi dengan lebar wajah maka akan ditemukan hasil 1,618.
2. Menjadi kiblat arsitektur dan seni
Banyak teori yang berupaya untuk dapat membuktikan bahwa deret ini dan juga golden ratio merupakan pola yang dapat mempengaruhi pikiran manusia sejak lama yang mungkin terjadi tanpa disadari. Banyak orang yakin dengan mengiblatkan desain karya seni pada pola golden ratio merupakan cara untuk dapat mencapai tingkat estetika yang tinggi
Hal ini lantaran dasar golden ratio ini memang sudah melekat secara alami dengan pikiran manusia. Sehingga kita akan dengan mudah akrab dan memahami bentuk estetika yang ingin disampaikan dengan proporsi yang sempurna.
3.Merumuskan pusat dunia
Melalui angka golden ratio akhirnya banyak pendapat yang menyimpulkan bahwa Kota Suci Mekkah merupakan pusat bumi karena jarak antara Mekkah-Kutub Utara dengan Mekkah-Kutub Selatan adalah 1,618.
Demikianlah penjelasan mengenai deret dan juga bilangan Fibonacci. Perlu Sedulur ketahui bahwa deret Fibonacci Python juga digunakan dalam bahasa pemrograman. Sedangkan untuk manfaatnya dalam dunia trading biasanya menggunakan Fibonacci Retracement.
Mau belanja bulanan nggak pakai ribet? Aplikasi Super solusinya! Mulai dari sembako hingga kebutuhan rumah tangga tersedia lengkap. Selain harganya murah, Sedulur juga bisa merasakan kemudahan belanja lewat handphone. Nggak perlu keluar rumah, belanjaan pun langsung diantar.
Bagi Sedulur yang punya toko kelontong atau warung, bisa juga lho belanja grosir atau kulakan lewat Aplikasi Super. Harga dijamin lebih murah dan bikin untung makin melimpah.



