Rumus Luas Lingkaran dengan Cara Menghitung dan Contohnya

Lingkaran merupakan satu dari sekian banyak bangun datar yang ada selain segitiga, segiempat, trapesium, jajar genjang, dan belah ketupat. Lingkaran memiliki bentuk bundar, dua dimensi, tidak memiliki ruang ataupun volume.

Cara mencari angka lainnya juga berbeda satu sama lain. Dalam ilmu matematika, terdapat dua rumus utama dalam menghitung lingkaran, yaitu rumus keliling lingkaran dan rumus luas lingkaran.

Beberapa soal juga terkadang menanyakan rumus luas setengah lingkaran maupun rumus keliling setengah lingkaran. Tidak perlu khawatir, Sedulur dapat mempelajari semua materi di atas dengan membaca artikel berikutini. Simak baik-baik ya!

BACA JUGA: Rumus Tekanan Hidrostatis Beserta Konsep dan Contoh Soalnya

1. Pengertian lingkaran

Lingkaran adalah sebuah bangun datar yang menjadi kedudukan titik-titik yang berjarak sama terhadap suatu titik tertentu. Jarak yang sama dikenal sebagai jari-jari lingkaran, sedangkan titik-titik tertentu dikenal sebagai  pusat lingkaran.

Pengertian lain dari lingkaran yaitu sebuah garis lengkung yang bertemu pada kedua ujungnya dan memiliki titik yang letaknya sama jauh dari sebuah titik tertentu. Titik tertentu ini disebut sebagai pusat lingkaran, sedangkan garis lengkung yang bertemu pada kedua ujungnya disebut sebagai keliling lingkaran. 

Sementara itu, jarak dari suatu titik pada lingkaran ke titik pusat disebut dengan jari-jari lingkaran dan daerah yang dibatasi oleh lingkaran disebut sebagai bidang lingkaran. Dalam kehidupan sehari-hari, contoh benda yang memiliki bentuk lingkaran adalah meja, roda kendaraan, tampah, cincin, papan target panahan, dan koin logam.

2. Unsur-unsur lingkaran

1. Titik pusat lingkaran (p) merupakan sebuah titik yang terletak tepat ditengah-tengah lingkaran.

2. Jari-jari lingkaran (r) merupakan garis yang menghubungkan titik pada keliling lingkaran dengan titik pusat lingkaran.

3. Diameter lingkaran (d) merupakan panjang garis lurus yang menghubungkan dua titik pada keliling lingkaran yang melalui titik pusat lingkaran. Jari-jari lingkaran mempunyai nilai setengah dari diameter dan diameter mempunyai nilai dua kali jari-jari. Dengan demikian dapat ditulis d = 2r.

4. Busur lingkaran merupakan garis lengkung yang menjadi bagian dari keliling lingkaran. Busur lingkaran dibagi menjadi dua, yaitu busur kecil dan busur besar. Dinamakan busur kecil apabila panjangnya kurang dari setengah lingkaran, dan dinamakan busur besar jika panjangnya lebih dari setengah lingkaran.

5. Tali busur lingkaran yaitu ruas garis lurus yang tidak melewati titik pusat lingkaran tapi menghubungkan dua titik pada keliling lingkaran. Analoginya, tali busur lingkaran akan sama seperti tali busur panah.

6. Tembereng lingkaran merupakan daerah yang ada di dalam lingkaran dan dibatasi oleh tali busur serta busur lingkaran.

7. Juring lingkaran adalah daerah yang dibatasi oleh dua garis jari-jari dan sebuah busur lingkaran yang posisinya diapit oleh dua buah jari-jari tersebut. Juring lingkaran dibagi menjadi dua yaitu juring besar dan juring kecil.

8. Apotema merupakan jarak terpendek antara tali busur dengan titik pusat lingkaran. Garis apotema yaitu tegak lurus dengan tali busur.

9. Sudut pusat merupakan sudut yang terbentuk dari perpotongan dua buah jari-jari di titik pusat lingkaran.

10. Sudut keliling merupakan sudut yang terbentuk oleh pertemuan antara dua tali busur pada satu titik di keliling lingkaran.

3. Rumus keliling lingkaran

Untuk lebih jelas memahami rumus lingkaran, berikut ini adalah rumus keliling lingkaran. Rumus luas dan keliling lingkaran adalah rumus yang berbeda dalam penggunaannya.

Rumus keliling = π x d atau karena d = 2 x r 

Maka, bisa juga ditulis = π x 2 x r maupun 2 x π x r

Keterangan:

d = diameter
r = jari-jari
π = nilai phi (22/7 atau 3,14)

BACA JUGA: Rumus Gradien Beserta Contoh Soal dan Pembahasannya

4. Rumus luas lingkaran

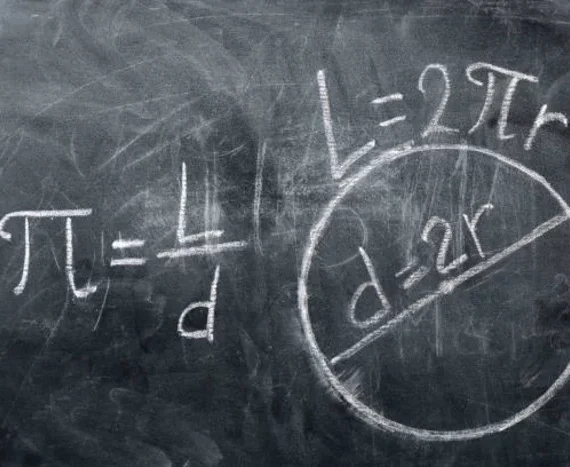
Sementara itu, rumus lingkaran diameter pada tidak digunakan dalam rumus luas lingkaran. Hal ini karena pada rumus luas, langsung menggunakan jari-jari kuadrat.

Rumus luas lingkaran = π x r² 

Keterangan:

π = nilai phi (3,14 atau 22/7)
r = jari-jari dari lingkaran

Tambahan, jika jari-jari memiliki satuan meter (m), maka satuan luasnya menjadi m² .

5. Rumus luas setengah lingkaran

Pada beberapa kasus, pasti ada lingkaran tak utuh, atau biasanya adalah setengah lingkaran. Berikut adalah dua rumus untuk mencari luas dan keliling setengah lingkaran.

1. Rumus luas setengah lingkaran

Luas = π r²  / 2

2. Rumus keliling setengah lingkaran

Keliling = π D / 2 atau π r

BACA JUGA: Regresi: Pengertian, Fungsi, Jenis, Manfaat dan Rumusnya

6. Contoh soal keliling lingkaran

1. Jika ada sebuah motor yang memiliki roda dengan jari-jari 21 cm, kemudian berputar sebanyak 2000 kali, maka berapakah jarak yang ditempuh oleh motor itu?

Jawab:

Jarak yang ditempuh motor sama dengan 2000 kali keliling lingkaran (roda)

Maka jarak yang ditempuh motor adalah

Keliling = 1000 x π x r

= 1.000 x 22/7 x 21 cm

= 66.000 cm = 66 km.

Jadi motor tersebut menempuh jarak sejauh 66 kilometer.

BACA JUGA: Hukum Ohm: Pengertian, Bunyi, Rumus dan Contoh Soalnya

7. Contoh soal luas lingkaran

1. Jika diketahui sebuah roda sepeda motor mempunyai diameter 42 cm. Maka, berapakah luas lingkaran roda tersebut!

Jawab: 

d = 42 cm
karena d = 2 kali nilai r, maka r sama dengan d dibagi 2. 

r = d/2
r = 42/2
r = 21 cm

Selanjutnya menghitung luas. Pada soal ini, rumus luas lingkaran diameternya diganti dengan jari-jari.

Luas = π x r² 
Luas = 22/7 x 21 x 21
Luas = 1386 cm² 

Jadi, luas roda sepeda motor tersebut adalah 1386 cm² .

8. Contoh soal luas dan keliling setengah lingkaran

1. Sebuah lingkaran memiliki jari-jari 14 cm. Apabila lingkaran tersebut dibagi menjadi dua bagian, maka berapakah luas setengah lingkaran tersebut? (diketahui π = 3,14)

Jawab:

Diketahui:

r = 20 cm
π = 3,14

Ditanya: Luas setengah lingkaran ?

Dijawab:

Luas setengah lingkaran = 1/2 x π x r² 
= 1/2 x 3,14 x 14² 
= 1/2 x 3,14 x 196
=  307,72 cm² 
Jadi, luas setengah lingkaran tersebut adalah 307,72 cm² .

2. Jika sebuah lingkaran dibagi menjadi dua bagian sama besar. Lingkaran tersebut memiliki diameter setengah lingkaran 14 cm dan π = 22/7. Maka, tentukanlah keliling setengah lingkaran tersebut!

Jawab:

Diketahui

d = 14 cm
maka,
r = 14/2 = 7 cm
π = 22/7

Ditanya: Keliling setengah lingkaran? 

Dijawab:
Keliling setengah lingkaran = π x r
= 22/7 x 7
= 22 cm
Jadi, keliling dari setengah lingkaran tersebut adalah 22 cm.

Sekian informasi mengenai rumus luas lingkaran beserta cara menghitung dan contoh soalnya. Semoga informasi ini dapat membantu Sedulur mengingat ilmu dasar saat belajar materi matematika dan mengasah kemampuan berhitung menjadi lebih baik lagi. Selamat belajar!