Kubus adalah salah satu bangun ruang yang cukup menarik. Kesemua sisinya sama besar, sehingga membentuk ruang yang sangat khas. Untuk membentuk kubus, Sedulur memerlukan jari jaring kubus enam persegi yang disusun sedemikian rupa hingga bisa disatukan dan membentuk bangun ruang.
Keenam persegi yang disusun tersebut disebut sebagai jaring-jaring kubus pdf. Ada banyak variasi susunan jaring-jaring yang bisa dibuat untuk membangun kubus. Nah, sebelum tahu variasinya, yuk sekalian belajar deretan fakta menarik seputar kubus.
BACA JUGA: Mengenal Ciri-ciri Bangun Ruang Beserta Sifat & Jenisnya
Apa itu kubus?

Kubus adalah objek 3 dimensi yang tersusun dari 6 persegi sama besar. Dari bentuknya tersebut, ia pun dikenal pula dengan nama heksahedron atau prisma segiempat. Contoh paling mudah dari bentuk kubus yang bisa Sedulur temukan di sekitar adalah dadu dan es batu (yang dicetak dengan cetakan kubus).
Karakter kubus

Ada beberapa sifat khusus kubus yang perlu Sedulur tahu, nih. Catat juga.
- Kubus memiliki 12 rusuk, 6 penampang atau permukaan, dan 8 sudut
- 6 penampang kubus haruslah kongruen, memiliki panjang dan lebar yang sama persis.
- Begitu pula dengan rusuknya yang juga sama panjang dan kedelapan sudutnya harus sama besar
- Kubus memiliki 12 garis diagonal sisi yang sama besar. Mereka adalah garis silang yang ditarik di tiap permukaan kubus
- Ada 4 diagonal ruang kubus yang panjangnya juga sama besar. Diagonal ruang ditarik dari satu sudut ke sudut lain yang berseberangan hingga seolah-olah membelah kubus 3D menjadi 2-4 bagian secara menyilang
- Sudut di antara tiap penampangnya adalah 90 derajat
- Setiap penampang berhadapan dengan empat penampang lain
- Setiap sudut bertemu dengan tiga penampang dan tiga rusuk
Jaring-jaring kubus

Seperti yang sudah disinggung sebelumnya, kubus terbentuk dari enam persegi yang disusun sedemikian rupa. Jaring-jaring ini bisa Sedulur dapatkan dengan membongkar bangunan kubus dan meratakannya menjadi model 2 dimensi. Jika itu terjadi, kita bisa melihat bahwa setidaknya satu tepi penampang persegi tersebut bertautan dengan penampang lainnya. Lebih jelasnya, Sedulur bisa melihat model di atas.
BACA JUGA: Rumus Luas Selimut Tabung dan Contoh Lengkap Soalnya
Varian jaring jaring kubus

Jika ditanya jaring-jaring kubus ada berapa? Setidaknya ada 11 variasi yang bisa dibentuk. Mereka berubah posisi, tetapi masih saling bertautan dan bila dilipat ke arah tertentu akan membentuk bangun ruang kubus.
Jika diperhatikan, 11 jaring-jaring kubus di atas mirip dengan pola pada permainan tetris. Intinya ada 6 persegi kongruen yang bertautan satu sama lain di setidaknya satu sisi. Bila diperhatikan pula dan dibayangkan bahwa mereka terletak dalam kolom dan baris seperti tabel, maka ada 4 kolom dan 2-3 baris yang terpakai.
Bedanya dengan balok

Jaring-jaring kubus dan balok memiliki kemiripan dari segi susunan. Mereka sama-sama memiliki enam penampang atau permukaan. Hanya saja, ukuran antar penampangnya tidak sama persis seperti konstruksi kubus. Ada dua macam ukuran penampang yang menyusun balok. Jadi, jika kubus hanya punya satu ukuran yang disebut dengan sisi. Balok memiliki tiga ukuran yaitu panjang, lebar, dan tinggi.
Volume kubus

Setelah tahu gambar jaring-jaring kubus, ini saatnya Sedulur memahami hitungan-hitungan yang berkaitan dengan kubus. Berikut kumpulan rumus kubus yang bisa diingat. Kita mulai dengan volume terlebih dahulu. Volume digunakan untuk menghitung isi dari kubus bila seumpama ia diisi oleh sesuatu, misalnya saja air.
Cara menghitungnya cukup mudah, sebenarnya semua volume memiliki rumus yang sama yaitu sebagai berikut.
Volume = luas alas x tinggi
Luas alas ini yang kemudian akan berbeda-beda pada tiap bangun ruang. Selain berbentuk segiempat, ada pula bangun ruang yang memiliki alas lingkaran seperti tabung atau segitiga seperti limas segitiga. Tinggi juga bisa bervariasi rumusnya tergantung pada bentuk bangun ruang yang hendak dihitung.
Ada beberapa bangun ruang yang tingginya harus ditentukan dengan rumus tertentu karena tidak tersedia langsung dari informasi yang diketahui. Untuk kubus, rumusnya menjadi sederhana karena sisi alas dan tingginya sama persis. Jadi, bisa dihitung menggunakan rumus berikut ini.
Volume kubus = sisi x sisi x sisi
atau
Volume kubus = s³
Contoh soal:
Diketahui kubus memiliki rusuk atau sisi sepanjang 4 cm
Maka, volume kubus tersebut adalah 4x4x4 = 64 cm³
BACA JUGA: Apa itu Aida: Pengertian, Rumusan, Konsep & Contohnya
Luas permukaan kubus
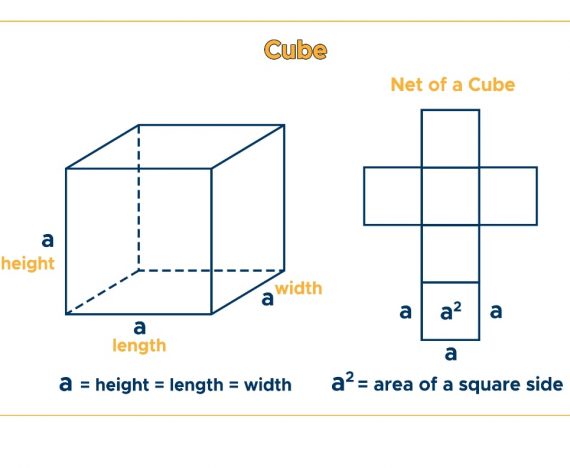
Secara umum, luas permukaan pada bangun ruang adalah penjumlahan dari total luas sisi. Dalam kasus kubus, luas permukaan adalah penjumlahan dari luas jaring-jaring kubus alas dan tutup ditambah sisi-sisinya. Sehingga, ada enam luas yang ditotal. Lagi-lagi mengingat sisi kubus sama persis, maka rumusnya bisa disimplifikasi menjadi berikut ini.
Luas permukaan = 6 (s x s) atau 6s²
Contoh soal:
Diketahui kubus memiliki rusuk atau sisi sepanjang 4 cm
Maka, luas permukaan kubus tersebut adalah 6 x 4² = 96 cm²
Tentunya rumus di atas hanya berlaku untuk kubus dan akan sangat berbeda untuk balok, kerucut, tabung, dan limas yang bentuknya lebih kompleks dan cara penghitungan luas permukaannya pun lebih rumit.
Menghitung diagonal sisi kubus
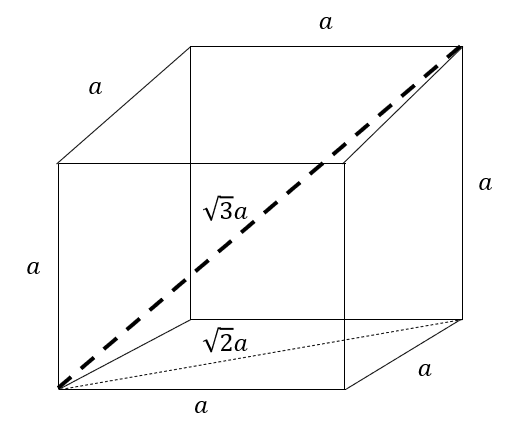
Hal lain yang bisa dihitung dari kubus adalah diagonal sisi, yaitu garis menyilang yang ditarik dari satu sudut ke sudut lainnya di penampang kubus. Bekal yang dibutuhkan adalah jaring-jaring kubus dan ukurannya. Ketika garis ditarik, maka terbentuk segitiga. Untuk itu, kita akan menggunakan rumus phytagoras untuk menentukan panjang garis diagonal tersebut yang dalam kasus kubus akan berbunyi seperti berikut.
Misal panjang diagonal sisi kita umpamakan sebagai D, dan sisi atau rusuk kubus kita sebut r
D² = r² + r²
D² = 2(r²) , maka bila ingin mencari D
D = √2r²
D = r√2
Untuk mendapatkan hasil dari diagonal sisi, biasanya Sedulur tidak perlu menghitung nilai dari √2. Jadi, seumpama panjang rusuk kubus adalah 8, maka ketika ditanya diagonal sisi cukup sebutkan 8√2.
BACA JUGA: Rumus Deret Geometri Beserta Pengertian dan Contoh Soalnya
Diagonal ruang kubus

Diagonal ruang kubus agak lebih kompleks karena ia ditarik menyilang di dalam bangun ruang, bukan hanya pada permukaan penampang kubus. Maka rumus yang dipakai sebagai berikut.
Umpamakan diagonal ruang adalah E dan diagonal sisi adalah D, sementara panjang sisi kubus adalah r, maka:
E² = D² + r²
E² = (r√2)² + r²
E² = 2r² + r²
E² = 3r²
E = √3r²
E = r√3
Sama dengan diagonal sisi, Sedulur juga tidak perlu menghitung nilai dari √3, kecuali bila diminta untuk mencari nilai yang mendekati.
Aplikasi dalam kehidupan nyata

Setelah tahu konstruksi jaring-jaring kubus, Sedulur tentu mulai berpikir apa sih sebenarnya aplikasi kubus dalam dunia nyata? Jawabannya bisa kamu temukan dari benda-benda di sekitarmu.Misalnya saja kotak kardus untuk mengirim paket, es batu, dadu, atau bahkan blok batu alam dan batako untuk bangunan.
Mungkin saat ini Sedulur belum membutuhkannya, namun penghitungan macam ini berguna dalam proses konstruksi bangunan di mana pengembang harus memperkirakan jumlah kubus atau balok yang dibutuhkan untuk membuat dinding atau partisi dari bata atau batako. Ia juga dibutuhkan pekerja logistik yang harus mengirim barang atau produknya dengan peti kemas.
Maka, volume peti kemas harus dicocokan dengan volume kardus produk yang akan diangkut untuk memperkirakan estimasi biaya, jumlah peti yang dibutuhkan dan lain sebagainya. Kubus memang tidak sepopuler balok yang lebih mudah kita temukan dalam barang sehari-hari macam oven, microwave, laci, lemari, dan lain sebagainya.
Penjelasan lengkap tentang jaring-jaring kubus dan sayapnya, serta berbagai rumusnya sudah Sedulur kantongi, nih. Semoga hal-hal seputar kubus tidak lagi membuatmu risau, ya. Kubus adalah level bangun ruang paling mudah, kok. Ada yang lebih rumit seperti tabung, kerucut, dan limas.
Sedulur yang membutuhkan sembako, bisa membeli di Aplikasi Super lho! Sedulur akan mendapatkan harga yang lebih murah dan kemudahan belanja hanya lewat ponsel. Yuk unduh aplikasinya di sini sekarang.



