Rumus deret geometri merupakan salah satu rumus yang wajib dipelajari dalam pelajaran matematika. Memang, bagi yang tidak menyukai matematika, geometri merupakan salah satu hal yang sulit. Namun berbeda dengan seseorang yang hobi dan menyukai matematika, bagian materi deret geometri merupakan hal menyenangkan.
Agar dapat membuat Sedulur lebih menyukai matematika dan dapat memahami rumus deret geometri dengan mudah, dalam kesempatan kali ini akan kita bahas seperti apa rumus geometri yang dimaksud. Yuk, mari kita mulai pembahasannya!
BACA JUGA: Konsep Hukum Newton: Bunyi, Rumus, & Contoh Penerapannya
Definisi rumus deret geometri

Deret geometri memiliki pola dengan barisan aritmatika. Pola bilangan geometri yaitu 2, 4, 8, 16. ara menemukan pola barisan geometri adalah membandingkan dua suku yang berurutan, seperti 4/2 = 2, 8/4 = 2, dan 16/2 =2. Hasil perbandingan dua suku berurutan di atas adalah 2 yang disebut dengan rasio.
Barisan dengan rasio seperti barisan bilangan di atas disebut dengan barisan geometri. Seperti yang sudah dijelaskan di atas, setiap barisan bilangan yang memiliki rasio merupakan barisan geometri. Secara matematika, barisan dan deret geometri adalah suatu barisan bilangan U1, U2, U3, …, Un apabila memenuhi U2/U1 = U4/U3 = … = Un/Un-1 = r, dengan r adalah rasio atau pembanding.
Rumus deret geometri

Setelah mengetahui definisinya, Sedulur juga harus tahu apa saja rumus deret geometri dan aritmatika. Untuk memudahkan Sedulur, bisa simak penjelasan di bawah ini:
- Barisan geometri: 2, 6, 18, 54, …
- Deret geometri: 2 + 6 + 18 = 54 + …
- Jumlah n suku pertama ditulis sn deret geometri. Jadi:
- S1 = U1 = 2
- S2 = U1 + U2 = 2 + 6 = 8
- S3 = U1 + U2 + U3 = 2 + 6 + 18 = 26
- S4 = U1 + U2 + U3 + U4 = 2 + 6 + 18 + 54 = 80
Rumus jumlah deret geometri
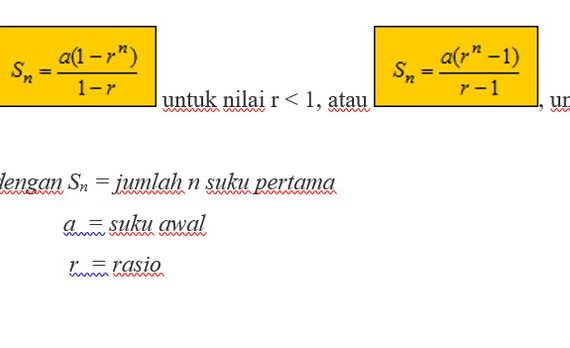
Sementara itu rumus jumlah n suku pertama berbeda dengan rumus deret geometri di atas. Sehingga rumus deret geometri tak hingga berdasarkan poin di atas, dapat diformulasikan sebagai berikut:
- Sn = U1 + U2 + U3 + … + Un
Sementara itu rumus suku ke-n barisan geometri ditemukan dengan suku tengah barisan geometri dapat dilihat dalam penjelasan di bawah ini:
- Sn = a + (ar) + (ar2) + … + arn-1
- r x Sn = (ar) + (ar2) + …. + arn-1 + arn
- Sn – r.Sn = a + 0 + 0 + + 0 + arn
- (1 – r)Sn = a – arn
- (1 – r)Sn = a (1 – rn)
BACA JUGA: Rumus Luas Selimut Tabung dan Contoh Lengkap Soalnya
Contoh soal deret geometri

Agar Sedulur dapat lebih memahami rumus deret geometri, Sedulur bisa menyimak contohnya di bawah ini. Dengan contoh di bawah ini, Sedulur bisa lebih mengimplementasikan rumus yang telah diurai sebelumnya.
1. Contoh soal 1
Berapakah jumlah dari 400 + 200 + 100 + 50 + 25 + 12,5 = …?
Jawaban:
- a = 400
- r = 200 : 400
- = 100 : 200
- = ½
- n = 6
Jadi jumlah dari 500 + 200 + 100 + 50 + 25 + 12,5 = 787,5
2. Contoh soal 2
Jika diketahui barisan ke-5 adalah 48 dan suku ke-8 adalah 384, maka suku ke-4 pada barisan bilangan tersebut?
Jawaban:
Barisan ke-5 yaitu:
- U5 = a.r^(5-1) = 48
- U4 = a.r^4 = 48
Suku ke-8:
- U8 = a.r^(8-1) = 384
- U8 = a.r^7 = 384
Maka, U8/U5 yaitu:
- (a.r^7) / (a.r^4) = 384 / 48
- r^3 = 8
- r = 2
Suku ke-5, menjadi:
- r = U5/U4
- U4 = U5/r
- U4 = 48/2
- U4 = 24
Jadi, suku ke-4 pada barisan bilangan geometri di atas adalah 24.
Itulah penjelasan terkait rumus deret geometri, semoga dengan penjelasan rumus deret geometri di atas, Sedulur bisa lebih mengetahui dan memahami deretan geometri menjadi lebih baik lagi. Dengan begitu Sedulur bisa mempelajarinya dengan mudah dan menguasainya dengan sempurna.
Sedulur yang membutuhkan sembako, bisa membeli di Aplikasi Super lho! Sedulur akan mendapatkan harga yang lebih murah dan kemudahan belanja hanya lewat ponsel. Yuk unduh aplikasinya di sini sekarang.



